SOLUTION: a quality control engineer inspects a random sample of three batteries from a lot of 30 cars batteries, which are ready to be shipped . if the such a lot contains ten batteries wit

Hi
30 Batteries (with 10 defects)  p(defect) = 1/3.  p(no defect) = 2/3
   3 chosen
p( 0 defects) = (2/3)^3 = 
Using
 
P(1 or 2 or 3 defects) =  3(1/3)(2/3)^2 + 3(1/3)^2(2/3) + (1/3)^3
                           = 12/27 + 6/27 + 1/27 = 
Or  1 - 8/27 = 19/27 (bit easier)

We have the set A of 30 items and its subset B of defective items consisting of 10 items.


We randomly select 3 items from the set A.


If no one of these 3 items is defective, it means that this triple of items is selected from the subset of 20 good items.



The probability to have good item at the first selection is  .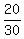

The probability to have good item at the second selection (having good item at the first selection) is  .

The probability to have good item at the third selection (having good items after the first and second selections) is  .


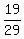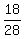The probability to have good triple is thus  the product 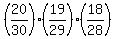  = 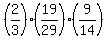 =  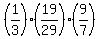=  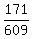= 0.2808  (rounded).


It is the answer to question (1).


The answer to question (2) is the COMPLEMENT  1 - 0.2808 = 0.7192  (rounded, too).

(1) The probability in this problem is the ratio of two numbers.

    The denominator is the number of all possible triples of batteries from 
    the whole set of 30 batteries.  The number of such triples is the number of all combinations

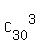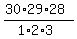         =  = 4060.


    The numerator of this fraction is the number of all triples comprising of good batteries.
    It is the number of combinations 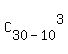  =  =  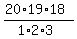= 1140.


    Thus the probability  P = P(1) = 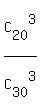 =  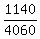=  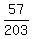= 0.2808  (rounded).    ANSWER



(2)  For the second question, the probability is the COMPLEMENT to what we found  above

         P(2) = 1 - P(1) = 1 - 0.2808 = 0.7192   (rounded).    ANSWER