Question 1197408: Andy is a restaurant owner. He believes 72% of his customers are satisfied with the food quality of his restaurant. From a random sample of 82 customers, what are the following probabilities? (Round your answers to four decimal places, if needed.)
(a) What is the probability that LESS than 60 customers are satisfied with the food quality?
(b) What is the probability that AT LEAST 60 customers are satisfied with the food quality?
(c) What is the probability that the sample proportion of customers who are satisfied with the food quality is between 70% and 77%?
Found 2 solutions by ikleyn, ewatrrr:
Answer by ikleyn(52806)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Andy is a restaurant owner. He believes 72% of his customers are satisfied
with the food quality of his restaurant. From a random sample of 82 customers,
what are the following probabilities? (Round your answers to four decimal places, if needed.)
(a) What is the probability that LESS than 60 customers are satisfied with the food quality?
(b) What is the probability that AT LEAST 60 customers are satisfied with the food quality?
(c) What is the probability that the sample proportion of customers who are satisfied
with the food quality is between 70% and 77%?
~~~~~~~~~~~~~~~~~~~
This problem is about a binomial distribution with large number of trials.
For such problems, the way to solve them is to use the fact that a binomial distribution
at large number of trials can be approximated by a normal distribution.
In more precise terms, the binomial distribution B(n trials; individual probability of success p)
can be approximated by the normal distribution with the mean m = p*n and the standard deviation
of 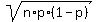 . .
For more info, see this link https://www.statology.org/normal-approximation/
So, to answer questions, we will consider the normal distribution with m = 82*0.72 = 59.04
and SD =  = 4.06586 (rounded). = 4.06586 (rounded).
(a) Thus, the probability that LESS than 60 customers are satisfied with the food quality is approximately
P_norm(X < 60; m = 59.04; SD = 4.06586).
It is the area under the specified normal curve on the left from the z-row mark z < 60.
You can use your standard calculator (function normalcdf(-9999,60,m,SD)) or online calculator
at the site https://onlinestatbook.com/2/calculators/normal_dist.html
In any case, your answer is P = 0.5933.
(b) In this case, the answer is, OBVIOUSLY, the complement to (a) 1 - 0.5933 = 0.4067.
(c) In this case, the answer is
P_norm(0.7*82 <= X <= 0.77*82; m= 59.04; SD= 4.06586) = P_norm(57.4 <= X <= 63.14; m= 59.04; SD= 4.06586)}}}.
It is the area under the specified normal curve between z-row marks 57.4 and 63.14.
Again, you can calculate it as normalcdf(-9999, 63.14, 59.04, 4.06586) - normalcdf(-9999, 57.4, 59.04, 4.06586),
or using the online calculator referred above.
In any case, the answer is P = 0.5.
Solved.
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Binomial distribution: p = .72, n = 82
Using TI or similarly an inexpensive calculator like an Casio fx-115 ES plus
P(n < 60) = binomcdf(n, p, largest x-value) = binomcdf(82,.72, 59) = .5379
P(n ≥ 60) = 1 - .5379 = .4621
P(70% ≤ x ≤ 77%)
IF this were a Normal Distribution:
P(70% ≤ x ≤ 77%) = normalcdf(smaller, larger, µ, σ).
Note: We can use the normal distribution as a close approximation to the
binomial distribution whenever np > 5 and nq > 5:( .72*82 = 59.04 and .28*82 = 22.96 )
P(70% ≤ x ≤ 77%) = normalcdf(smaller, larger, µ, σ)
=normalcdf(.70*82, .77*82, .72*82, √(82*.72*.28) = .5
|
|
|