SOLUTION: What are the side lengths of the right triangles of 45-45-90 and 30-60-90?

There is no fixed length for either of these triangles.  Rather, there is a RELATIONSHIP between the hypotenuse and shorter two sides.  For example, for a 45-45-90 triangle, the two shorter legs have equal length, and we can call this length L.  If we do this, the hypotenuse h has length  .



This follows from the Pythagorean Theorem  where for any right triangle, the hypotenuse is related to the other two sides, a and b, by:  







Back to the 45-45-90 triangle:  

 

  

 



So, if I pick L=10cm, h will be about 14.14cm

I can also pick L=23m, and h will then be 32.53m,  etc.

The important thing to note is both of these examples give you a 45-45-90 triangle.



---

For the 30-60-90 triangle,  h is as before (square root of sum of squares of shorter two sides) but the relation of h to the shorter two sides is as follows:



   a = h * sin(30) = 

   b = h * cos(30) = 



where  a is the side opposite the 30 degree angle, and b is the side adjacent to the 30 degree angle (such that the 30 degree angle comes between 'b' and 'h').



Notice for the 30-60-90 triangle, the Pythagorean Theorem still holds, as it does for all right triangles:

      h =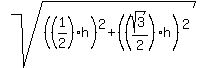   

        = 

        = 

        =     





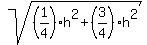
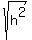
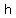
Hope this helps!