SOLUTION: There is a .02 probability that a customer's Visa charge will be rejected at a certain Target store because the transaction exceeds the customer's credit limit. What is the expecte

Algebra ->  Probability-and-statistics -> SOLUTION: There is a .02 probability that a customer's Visa charge will be rejected at a certain Target store because the transaction exceeds the customer's credit limit. What is the expecte      Log On


   

Question 1197331: There is a .02 probability that a customer's Visa charge will be rejected at a certain Target store because the transaction exceeds the customer's credit limit. What is the expected number of Visa transactions until the first one is rejected?
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
There is a .02 probability that a customer's Visa charge will be rejected
at a certain Target store because the transaction exceeds the customer's credit limit.
What is the expected number of Visa transactions until the first one is rejected?
~~~~~~~~~~~~~~~ 

P(rejected right at the 1st use)               = 0.02.

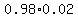P(rejected at the 2nd use) = %281-0.02%29%2A0.02   = 0.98%2A0.02

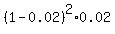P(rejected at the 3rd use) = %281-0.02%29%5E2%2A0.02 = 0.98%5E2%2A0.02

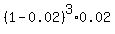P(rejected at the 4th use) = %281-0.02%29%5E3%2A0.02 = 0.98%5E3%2A0.02

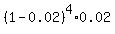P(rejected at the 5th use) = %281-0.02%29%5E4%2A0.02 = 0.98%5E4%2A0.02

  . . . . . .                    . . . . . .            . . . . . . 


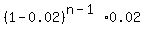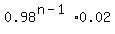P(rejected at the nth use) = %281-0.02%29%5E%28n-1%29%2A0.02 = 0.98%5E%28n-1%29%2A0.02

  . . . . . .                    . . . . . .            . . . . . . 


So, the Math expectation ME is this sum

    ME =  = 

       = 0.02%2Asum%28n%2A0.98%5En%2C+n=1%2Cinfinity%29


It is well known fact that the sum  sum%28n%2Ax%5En%2C+n=1%2Cinfinity%29   is   x%2F%28x-1%29%5E2.


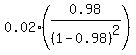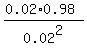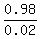So, in our case  ME = 0.02%2Asum%28n%2A0.98%5En%2C+n=1%2Cinfinity%29 = 0.02%2A%280.98%2F%281-0.98%29%5E2%29 = %280.02%2A0.98%29%2F0.02%5E2 = 0.98%2F0.02 = 49.


ANSWER.  The expected number of Visa transactions until the first one is rejected is 49.

Solved.

Notice that the answer is consistent with the fact that   49 = 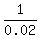1%2F0.02 - 1 = 50 - 1,   which confirms the answer.


-----------------


Regarding the formula for the sum   sum%28n%2Ax%5En%2C+n=1%2Cinfinity%29 = x%2F%28x-1%29%5E2,   below I deduce it. 

Let 

    S = x + 2x^2 + 3x^3 + 4x^4 + . . .      (1)

Multiply by x both sides,

   xS =      x^2 + 2x^3 + 3x^4 + . . .      (2)


From equation (1), subtract equation (2).  You will get

   S(1−x) = x + x^2 + x^3 + x^4 + . . . 

   S(1−x) = 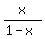x%2F%281-x%29

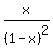   S      = x%2F%281-x%29%5E2.

QED.