.
There are 1859 balls inside an urn from 1 to 1859. A ball is selected at random.
Given that the selected ball has a number that is not relatively prime to 1859,
what is the probability that it is divisible by 13 only?
~~~~~~~~~~~~~~
The prime decomposition of the number 1859 is
1859 =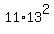 
. (1)
To find this prime decomposition quickly and without tortures,
ask GOOGLE "primary decomposition of the number 1859".
You will get web-sites with online solvers, which provide the answer to you in one second.
Concretely, this web-site gives the answer https://www.factors-of.com/Prime-decomposition-of_1859_
Alternatively, you can find prime divisors manually using sieve of Eratosthenes.
You are given that randomly selected ball has a number that is not relatively prime to 1859.
It means that this randomly selected number is divisible by 11 or by 13 (or both).
The subset N(11) of integers from {1,2,3, . . . ,1859} that are divisible by 11, has 1859/11 = 169 elements.
The subset N(13) of integers from {1,2,3, . . . ,1859} that are divisible by 13, has 1859/13 = 143 elements.
The subset N(11*13) of integers from {1,2,3, . . . ,1859} that are divisible by both 11 and 13, has 1859/(11*13) = 13 elements.
(this subset is the intersection of N(11) and N(13), since 11 and 13 are relatively prime).
The subset N(11,13) of integers from {1,2,3, . . . ,1859} that are not relatively prime to 1859 is the union of N(11) and N(13)
and has N(11) + N(13) - N(11*13) = 169 + 143 - 13 = 299 elements.
It is the "given" subset, to which the selected number
does belong, as it is given in the condition.
The subset of N(11,13) which consists of integers divisible by 13 only is N(13) \ N(11*13), and it has 143 - 13 = 130 elements.
The probability under the problem's question is this ratio P = 
= 
.
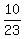Solved.
