Question 1197060: There are 1859 balls inside an urn from 1 to 1859. A ball is selected randomly. What is the probability that the selected ball has a number that is relatively prime to 1859?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52847)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Two numbers are relatively prime, aka coprime, if the only factor they have in common is 1.
In other words, if the GCF is 1, then the numbers are coprime.
Example: 15 and 34 are relatively prime
Determine the prime factorization of 1859
1859 = 11*13*13 = 11*13^2
If an integer x is coprime with 1859, then it won't have any of 11 or 13 as part of its factorization.
If x is not coprime with 1859, then it will have at least one or more of the factors mentioned.
set A = multiples of 11, from 11 to 1859
set B = multiples of 13, from 13 to 1859
set C = multiples of 11*13, from 143 to 1859
11*13 = 143 is the LCM of 11 and 13
A = {11*1, 11*2, 11*3, ..., 11*169}
B = {13*1, 13*2, 13*3, ..., 13*143}
C = {11*13*1, 11*13*2, 11*13*3, ..., 11*13*13} = {143*1, 143*2, 143*3, ..., 143*13}
Claim1: C is a subset of A, and C is a subset of B
Claim2: All values in sets A,B,C are not relatively prime to 1859
Claim3: All values in sets A,B,C consist of all non-relatively prime values from 11 to 1859
I'll let the student prove these claims.
There are 169 items in set A
There are 143 items in set B
That's 169+143 = 312 values
But as the claim1 mentions, C is a subset of A and B.
In other words, A and B have an overlap of values which reside in set C
Each item in set C is of the form 11*13*m where m ranges from m = 1 to m = 13.
Set C has 13 items inside it
Subtract 13 from 312 to find the number of unique items in either set A or set B or both
312 - 13 = 299
There are 299 values that aren't relatively prime to 1859, and these values go from 11 to 1859.
Think of it like this
n(A or B) = n(A) + n(B) - n(A and B)
n(A or B) = 169 + 143 - 13
n(A or B) = 299
There are 299 values in set A, set B, or both
Since there are 299 values that aren't relatively prime with 1859, this means there must be 1859-299 = 1560 items that are relatively prime to 1859.
Side note:
The totient function counts how many values are relatively prime to n, where we go from 1 to n
Typing "totient(1859)", without quotes, into WolframAlpha gets us the result 1560
https://www.wolframalpha.com/input?i=totient%281859%29
Here's an article talking about the totient function in more detail
https://mathworld.wolfram.com/TotientFunction.html
The formula to calculating totient(1859) is to compute 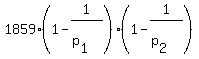 where where  and and  are the prime factors 11 and 13 in this case. Which means we have totient(1859) = are the prime factors 11 and 13 in this case. Which means we have totient(1859) = 
So we have 1560 relatively prime values we want out of 1859 values total in {1,2,3,...,1858,1859}
The probability we're after is 1560/1859 = (13*120)/(13*143) = 120/143
Answer = 120/143
|
|
|