|
Question 1196904: Solve each inequality, express the solution set in interval notation, then graph the solution set.
1.
2x/x−7 ≤ 5
Found 4 solutions by Alan3354, ikleyn, greenestamps, MathTherapy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve each inequality, express the solution set in interval notation, then graph the solution set.
2x/x−7 ≤ 5
~~~~~~~~~~~~~~~~~~~
The solution by Alan is incorrect.
It is incorrect because multiplying by (x-7) both sides of the given inequality
without changing the inequality sign is valid ONLY if x-7 > 0.
So, the Alan's solution is valid only if x > 7 and it produces then the solution set x >= 35/3.
Thus, when x > 7, the solution set in this domain is { x >= 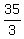 }. }.
It is the part, that Alan found out.
But it is only one part of the work which should be done.
In addition, the case x-7 < 0 should be (and MUST be) analyzed separately.
I do it below.
So, we assume now that x-7 < 0, which means x < 7.
Multiply both sides of the given inequality by (x-7).
Since this factor (x-7) is NEGATIVE now, we should change the sign of the inequality.
Thus after multiplying we have
2x >= 5*(x-7).
Simplify and solve for x
2x >= 5x - 35
35 >= 5x - 2x
35 >= 3x
x <= 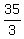 Thus in the case when x < 7, we have second inequality x <=
Thus in the case when x < 7, we have second inequality x <= 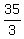 .
Thus, the second solution subset is {x < 7}.
Finally, from two basic cases, the solution set
consists of two subsets x >= .
Thus, the second solution subset is {x < 7}.
Finally, from two basic cases, the solution set
consists of two subsets x >= 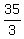 and x < 7.
In other words, the solution set is the union (-oo,7) U [ and x < 7.
In other words, the solution set is the union (-oo,7) U [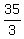 ,oo).
This solution set is plotted below
==============|============)--------------|==================
-oo 0 7 ,oo).
This solution set is plotted below
==============|============)--------------|==================
-oo 0 7 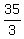 oo oo
Solved, and fully explained.
------------------
That mistake that Alan did, the beginner students make every day,
until a teacher or an expert will show them a right way solving such inequalities.
So, I am glad to have this opportunity to explain the things to you.
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
As tutor @ikleyn points out, if you solve the inequality by multiplying both sides of the inequality by x-7, then you need to consider two separate cases -- where x-7 is positive, and where it is negative.
Here is an alternative method for solving this kind of problem. Note in this example the algebra is probably more complicated with this method than with the other; however, it is a useful method to know, and in many similar problems the work required with this method will be easier.
Instead of multiplying both side of the inequality by anything, rewrite the inequality with only "0" on the right; then analyze the resulting rational function to find where the inequality is satisfied.





The critical points of that rational function are where the numerator or denominator is zero. The function value is 0 at x=35/3 and undefined at x=7.
Using test points on the three intervals determined by the critical points, and observing whether the function is 0 or undefined at those critical points, the solution to the inequality is
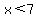 U U 
A graph, showing  (red) being less then 5 (green) for values of x less than 7 and greater than 35/3: (red) being less then 5 (green) for values of x less than 7 and greater than 35/3:
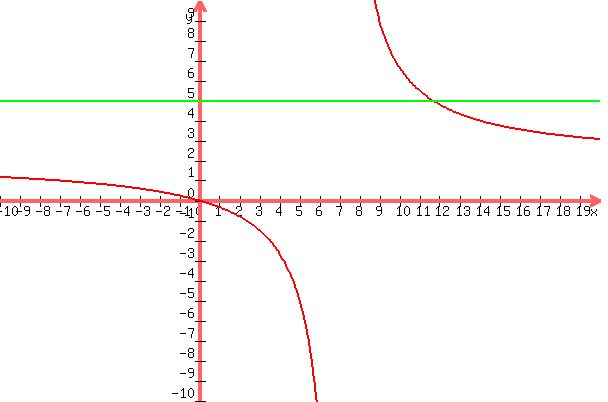
Finally, to be technically correct in a response to your question, we should note that the above discussion (and in the responses from the other tutors) is NOT for the inequality you posted. The inequality you posted, "2x/x−7 ≤ 5", is
 --> -->  --> --> 
which is true for all values of x for which it is defined -- i.e., for all x except x=0.
I bother to make this point because, if you are working on a problem like this, then your level of mathematical knowledge should be enough to know that the proper use of parentheses is important....
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solve each inequality, express the solution set in interval notation, then graph the solution set.
1.
2x/x−7 ≤ 5Solve each inequality, express the solution set in interval notation, then graph the solution set.
1.
2x/x−7 ≤ 5
It's very like that it's  , with , with  , since 7 will make the denominator UNDEFINED.
2x ≤ 5(x - 7) ------ Multiplying by LCD, (x - 7)
2x ≤ 5x - 35
2x - 5x ≤ - 35
- 3x ≤ - 35 , since 7 will make the denominator UNDEFINED.
2x ≤ 5(x - 7) ------ Multiplying by LCD, (x - 7)
2x ≤ 5x - 35
2x - 5x ≤ - 35
- 3x ≤ - 35
 Now, we have 2 critical points:
Now, we have 2 critical points:  and 3 TEST POINTS for x: and 3 TEST POINTS for x:  When the intervals are tested, we see that
When the intervals are tested, we see that  are the 2 solution-intervals.
Therefore, in INTERVAL NOTATION, we get: ( are the 2 solution-intervals.
Therefore, in INTERVAL NOTATION, we get: ( ) ) [ [ ) )
|
|
|
| |