Question 1196851: Find the domain and range of f(x) =(x+1)^(x-1)
Found 2 solutions by greenestamps, ewatrrr:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Clearly x = -1 is a critical value in determining the domain and range.
At x = -1, the function is

which is undefined.
So x = -1 is not in the domain.
For any value of x greater than -1, the expression is a power of a positive number, so the function value can always be evaluated. So (-1, infinity) is at least part of the domain.
The tricky part of determining the domain is with values of x less than -1. That results in a negative number raise to a negative power.
A negative number raised to a negative power is a real number if and only if the power is an integer. For example...

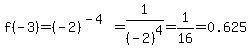

But for non-integer values of x less than -1, the function value is not a real number.
So....
Depending on your definition of domain, the domain of the function is either
(-1,infinity)
or
(-1,infinity) U {integers less than -1}
For the range, unless you know some very high-level mathematics, you can use a graphing calculator to find the answer. It should be clear that there is no upper limit to the range; my TI-83 calculator shows a minimum value of approximately 0.815154 at approximately x=0.454731.
So the range is approximately (0.815154,infinity).
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(x) =(x+1)^(x-1)
as You can see on graph: Domain: x can be any real number > -1
Using 'calculate' on graphing software, when f'(x) = 0, f(x) = .8165est
Range: f(x) >= .8165est See 2nd graph


|
|
|