Question 1196827: A right triangle has a hypotenuse of 1. One leg is x. The other leg is (x - 7).
Find the area of the triangle.
Found 3 solutions by josgarithmetic, ikleyn, math_tutor2020:
Answer by josgarithmetic(39617)   (Show Source):
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
A right triangle has a hypotenuse of 1. One leg is x. The other leg is (x - 7).
Find the area of the triangle.
~~~~~~~~~~~~~~~~
Such a triangle does not exist.
Proof: the difference of two sides, x and x-7, must be less than the third side (from the triangle's inequality).
But the difference of the sides x and (x-7) is 7, while the third side is 1.
Contradiction.
As it is worded, printed and posted, this "problem " is dead just from the very moment of its creation.
/////////////////
Comment from student : You are right. It was a typo. Here it is:
Hypotenuse = x + 1 One side = x Other side = x - 7 Find the area.
My response : It is just another story. See my solution below.
Write the Pythagorean equation
x^2 + (x-7)^2 = (x+1)^2.
Simplify and find x
x^2 + (x^2 - 14x + 49) = x^2 + 2x + 1
x^2 - 16x + 48 = 0
(x-4)*(x-12) = 0.
For x, we have two roots: x= 4 and x= 12.
The root x= 4 is not the solution, since then x-7 is negative.
The root x= 12 produces the right angled triangle (5,12,13).
Its area is 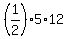 = 5*6 = 30 square units. ANSWER
Solved.
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
Edit: Disregard my entire solution, since the premise is based on a typo in the original question posted. Refer to the solution @ikleyn has posted.
Use the pythagorean theorem  to form the equation 
That equation solves to these complex values
 and 
Use the quadratic formula.
This shows that we don't get a real number for x and therefore such a right triangle isn't possible.
------------------------------------------------------
Or you could use the triangle inequality theorem
a = x
b = x-7
c = 1
This theorem says the sum of any two sides must exceed the third side if we want a triangle to be possible- a+b > c leads to x+x-7 > 1 which solves to x > 4
- a+c > b leads to x+1 > x-7 which leads to 1 > -7; while it's nice we get a true inequality statement, it's not particularly useful here, so we'll move on
- b+c > a leads to x-7+1 > x which leads to -6 > 0 which is false
The 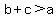 case leads to a contradiction.
We have the two sides b = x-7 and c = 1 combine to x-6 which is NOT larger than the third side a = x
Let's replace x with an actual number greater than 7
Let's go for x = 10
So,
a = x = 10
b = x-7 = 10-7 = 3
c = 1
Then notice
b+c = 3+1 = 4 is NOT larger than a = 10
Try this out using slips of paper of lengths 10, 3 and 1 (inches, cm, or whatever your favorite unit is)
You'll find a triangle is impossible to form here.
------------------------------------------------------
Here's an interactive GeoGebra tool to play with
https://www.geogebra.org/m/yzv48tkk
If the applet doesn't load, then hover your mouse over the center and click on the curved arrow. It should refresh. If not then let me know and I'll try to fix the issue the best I can.
In that applet, we have the three sides {1,3,10}
segment AB = 10
segment AD = 1
segment BC = 3
The dashed circles show all possible locations the points D and B could go. In other words, segment AD swings around point A; while segment BC swings around point B.
No matter how hard we try, there is no way to join up points C and D to form a triangle. The sides AD = 1 and BC = 3 are simply too short to add to something larger than AB = 10
|
|
|
