SOLUTION: Verify that the points (2, -1), (5, 5) and (6, -3) is a right triangle.

Algebra ->  Pythagorean-theorem -> SOLUTION: Verify that the points (2, -1), (5, 5) and (6, -3) is a right triangle.       Log On


   

Question 1196826: Verify that the points (2, -1), (5, 5) and (6, -3) is a right triangle.

Found 2 solutions by josgarithmetic, math_tutor2020:
Answer by josgarithmetic(39628) About Me  (Show Source):
You can put this solution on YOUR website!
SLOPES of every pair of points - exactly two pair of points will have slopes which are negative reciprocals.



%285%2B1%29%2F%285-2%29=6%2F3=2;
%28-3-5%29%2F%286-5%29=-8;
%28-3%2B1%29%2F%286-2%29=-2%2F4=-1%2F2

Yes. The point (2,-1) is the vertex with the right-angle.

---
---

YOU WISH TO VERIFY THAT THE THREE POINTS FORM A RIGHT TRIANGLE.
YOU FIND BY SLOPE CALCULATION THAT 2%2A%28-1%2F2%29=-1 FOR TWO OF THE PAIR OF POINTS----THAT IS YOUR VERIFICATION.

Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Define the points as A,B,C
The order of the labels doesn't matter

A = (2,-1)
B = (5,5)
C = (6,-3)

Let's find the slope of segment AB
We'll use the aptly named slope formula (see footnote at the very bottom of the page).
m+=+%28y%5B2%5D+-+y%5B1%5D%29%2F%28x%5B2%5D+-+x%5B1%5D%29

m+=+%285+-+%28-1%29%29%2F%285+-+2%29

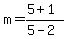
m+=+%285+%2B+1%29%2F%285+-+2%29

m+=+%286%29%2F%283%29

m+=+2
The slope of segment AB is 2 = 2/1
Each time we move up 2 units, we move to the right 1 unit.
In short: "Up 2, right 1".

Repeat the same idea for the other segments of triangle ABC
I'll let you do those steps, but here are the slope values so you can check your work:
slope of BC = -8
slope of AC = -1/2

--------------------------------------------------

Let's tidy everything up in a summary so far:
slope of AB = 2
slope of BC = -8
slope of AC = -1/2

Now ask yourself: "are there any 2 slopes that pair up to multiply to -1?"
The answer is "yes" because the slopes of AB and AC multiply to 2*(-1/2) = -1

This is sufficient information to show AB is perpendicular to AC. The two segments meet up at a 90 degree angle (aka right angle). This shows we have a right triangle. The 90 degree angle is located at point A since AB and AC share this letter in common.

--------------------------------------------------

note: if one segment is vertical, then finding the slope is impossible. The slope of a vertical line is undefined. But if you can show one line is vertical and another horizontal, then you'd have a right triangle. All horizontal lines have slope 0.