|
Question 1196810: A Ferris wheel is 29 meters in diameter and boarded from a platform that is 1 meter above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 16 minutes. The function h(t) gives a person’s height in meters above the ground t minutes after the wheel begins to turn.
a. Find the amplitude, midline, and period of h(t).
b. Assume that a person has just boarded the Ferris wheel from the platform and that the Ferris wheel starts spinning at time t=0 . Find a formula for the height function h(t) .
c. If the Ferris wheel continues to turn, how high off the ground is a person after 60 minutes?
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A Ferris wheel is 29 meters in diameter and boarded from a platform that is 1 meter above the ground.
The six o’clock position on the Ferris wheel is level with the loading platform.
The wheel completes 1 full revolution in 16 minutes. The function h(t) gives a person’s height
in meters above the ground t minutes after the wheel begins to turn.
(a) Find the amplitude, midline, and period of h(t).
(b) Assume that a person has just boarded the Ferris wheel from the platform
and that the Ferris wheel starts spinning at time t=0 .
Find a formula for the height function h(t) .
(c) If the Ferris wheel continues to turn, how high off the ground is a person after 60 minutes?
~~~~~~~~~~~~~~~~~~~
(a) The amplitude A is equal to the radius of the wheel, i.e. A = 29/2 = 14.5 meters.
Midline is the height of the center of the wheel  , i.e. 1 + 14.5 = 15.5 meters.
The period T is the time of one revolution, i.e. T = 16 minutes.
(b) The plot of the function h(t) is a cosinusoid taken with the "-" (minus) sign
h(t) = - , i.e. 1 + 14.5 = 15.5 meters.
The period T is the time of one revolution, i.e. T = 16 minutes.
(b) The plot of the function h(t) is a cosinusoid taken with the "-" (minus) sign
h(t) = -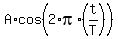 + +  ,
where A is the amplitude, T is the period, t is the current time and ,
where A is the amplitude, T is the period, t is the current time and  is
the midline's vertical coordinate.
With the given data, the equation is
h(t) = - is
the midline's vertical coordinate.
With the given data, the equation is
h(t) = -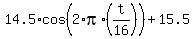 meters.
(c) 60 minutes is 12 minutes after three full revolution;
the ratio meters.
(c) 60 minutes is 12 minutes after three full revolution;
the ratio 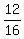 is is  of the period, so the height of the wheel at 60 minutes is
h(60) = - of the period, so the height of the wheel at 60 minutes is
h(60) = -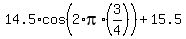 = - = - = 0 + 15.5 = 15.5 meters.
The position of the person is 3/4 of the cycle on the Ferris wheel circumference,
so the height of the person over the ground is the same as the height of the center of
the wheel over the ground. = 0 + 15.5 = 15.5 meters.
The position of the person is 3/4 of the cycle on the Ferris wheel circumference,
so the height of the person over the ground is the same as the height of the center of
the wheel over the ground.
Solved.
|
|
|
| |