Question 1196797: This year, alex's grandfather's age is 6 times of Alex's age. After a few years, Alex's grandfather's age will be 5 times of Alex's age. After another few years, Alex's grandfather's age will be 4 times of Alex's age. What is Alex's grandfather's age this year?
Found 3 solutions by math_tutor2020, ankor@dixie-net.com, MathTherapy:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Please define what you mean by "few". That term is a bit vague. In some situations, it could mean 3. But perhaps the author intends some other number instead.
Edit: Here are two possible scenarios
| Alex | Grandpa | Ratio | | This year | 12 | 72 | 72/12 = 6 | | 3 years from now | 15 | 75 | 75/15 = 5 | | 8 years from now | 20 | 80 | 80/20 = 4 |
and
| Alex | Grandpa | Ratio | | This year | 24 | 144 | 144/24 = 6 | | 6 years from now | 30 | 150 | 150/30 = 5 | | 16 years from now | 40 | 160 | 160/40 = 4 |
The grandpa's ages in the second table are either impossible or very unlikely.
As of the year 2022, the oldest recorded age is 122.
However, with modern medicine getting better and better, perhaps ages like 144, 150, and 160 won't be too crazy in the (near) distant future.
Your teacher probably is going to side with the first table if anything.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! This year, alex's grandfather's age is 6 times of Alex's age.
After a few years, Alex's grandfather's age will be 5 times of Alex's age.
After another few years, Alex's grandfather's age will be 4 times of Alex's age.
What is Alex's grandfather's age this year?
:
let a = Alex's present age
Grandfather is 6 time Alex's, therefore:
let 6a = grandfathers present age
:
let y = "another few years"
let x = a few more years
:
"another few years" equation
6a + y = 5(a+y)
6a + y = 5a + 5y
6a - 5a = 5y - y
a = 4y
:
a "few more years" equation
6a + x = 4(a+x)
6a + x = 4a + 4x
6a - 4a = 4x - x
2a = 3x
a = 1.5x
:
a = a, therefore
4y = 1.5x
we want integers here, therefore
8y = 3x
y = 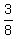 x x
y and x have to be single digit integers therefore
y = 3 yrs and x = 8 yrs
:
find a
a = 4y
a = 4(3)
a = 12 yrs is Alex's age
then
6(12) = 72 yrs is grandfather's age
You can substitute in the 3 yr and 8 yr equations to confirm this
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! This year, alex's grandfather's age is 6 times of Alex's age. After a few years, Alex's grandfather's age will be 5 times of Alex's age. After another few years, Alex's grandfather's age will be 4 times of Alex's age. What is Alex's grandfather's age this year?
Let grandfather’s age be G
Then Alex’ is 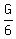 Let “a few years” be y. Then:
Let “a few years” be y. Then:  Let “another few years,” or years after this year, be z. Then: Let “another few years,” or years after this year, be z. Then:  We then get:
We then get:  With
With  , ONLY MULTIPLES of 3 can be substituted for y in order to get INTEGER-VALUES for z
Therefore, if y = 3, then , ONLY MULTIPLES of 3 can be substituted for y in order to get INTEGER-VALUES for z
Therefore, if y = 3, then  This gives us: G, or the grandfather’s age as: 24(3), or 9(8) = 72.
With ONLY MULTIPLES of 3 that can be substituted for y, we substitute 6 for y to get:
This gives us: G, or the grandfather’s age as: 24(3), or 9(8) = 72.
With ONLY MULTIPLES of 3 that can be substituted for y, we substitute 6 for y to get:  This gives us: G, or the grandfather’s age as: 24(6), or 9(16) = 144
As it’s HIGHLY UNLIKELY that the grandfather is 144 years old, no LARGER multiples of 3 need to be tried/substituted.
Therefore, the more REALISTIC age for him is as stated above, 72.
This gives us: G, or the grandfather’s age as: 24(6), or 9(16) = 144
As it’s HIGHLY UNLIKELY that the grandfather is 144 years old, no LARGER multiples of 3 need to be tried/substituted.
Therefore, the more REALISTIC age for him is as stated above, 72.
|
|
|