SOLUTION: What is the missing term of the geometric sequence {-3,_,-108}?

You have  = -3

and  = -108



so    -->  r = 6,  this is the common ratio (the number by which you multiply  to get  )



The missing term is  = 



{ -3, -18, -108 } 

You are given the 1st and the 3rd terms of a geometric progression, and they ask you about the 2nd term.


In any geometric progression, any term, which has neighbors terms on the left and on the right, is the geometric mean of the neighbors terms

     = .


In your case,

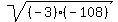     =  = = +/- 18.


Square root of a positive number has two values, one positive and one negative, 
so you have two possible values 18 and -18 for the term    in the middle.


Accordingly, there are 2 (two) possible progressions:


    one progression is  -3, 18, -108  with the common ratio -6,

    and another progression  -3, -18, -108  with the common ratio 6.

          

         ------ Cross-multiplying  

      
Term 2, or 

OR

        or