Question 1196650: Determine whether function;f(x) =(-1)^[x] is even,odd or neither of two (where[]denotes the greatest integer function).
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52754)   (Show Source):
You can put this solution on YOUR website! .
Determine whether function f(x) =(-1)^[x] is even, odd or neither of two
(where [] denotes the greatest integer function).
~~~~~~~~~~~~~~~~~
DEFINITION: Greatest Integer Function
The greatest integer function is also known as the step function. It RETURNS the number which is the nearest integer
less than or equal to the given number. The greatest integer function has a step curve
The domain of the greatest integer function is ℝ and its range is ℤ.
Therefore the greatest integer function is simply rounding off the given number to the greatest
integer that is less than or equal to the given number.
See the link https://www.cuemath.com/algebra/greatest-integer-function
------------------------------------------------------------------------
Let's consider our function at x= 1.2.
Then [x] = [1.2] = 1. THEREFPRE, f(x) =  = -1.
At x= -1.2, we have [x] = [-1.2] = -2. THEREFORE, f(x) = f(-1.2) = 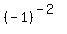 = 1.
Since f(1.2) =/= f(-1.2), f(x) is not an even function.
Let's consider our function at x= 2.
Then [x] = [2] = 2. THEREFPRE, f(x) = 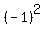 = 1.
At x= -2, we have [x] = [-2] = -2. THEREFORE, f(x) = f(-2) = 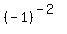= 1.
Since f(-2) =/= -f(-2), f(x) is not an odd function.
So, the conclusion is that given function f(x) is NEITHER even NOR odd.
Completed, proved and explained.
////////////////////////
The logic and the reasoning in the post by @MathLover1 are defective and lead you to NOWHERE.
So, you better ignore her post, for your safety.
\\\\\\\\\\\\\\\\\\\\\\\\\
This problem is tricky: on the set of integer numbers, function f(x) is EVEN.
It is because for integer x, the number x is always the same as [x], so [x] and [-x] always have the same parity.
On the set of all other real numbers (others than integers), function f(x) is ODD.
It is because for non-integer x, the number [x] always has different parity than [-x].
Considered on the total set of all real numbers, function f(x) is NEITHER even NOR odd, as I said it in my post.
The cause for it is that the function [x] itself is NEITHER even NOR odd on the set of all real numbers.
Answer by MathLover1(20849)  (Show Source):
|
|
|
