Question 1196642: HERE IS THE TABLE: https://imagizer.imageshack.com/img923/3314/zi0hjD.jpg
A sample of 1793 homes in a neighborhood of a large city during a recent year produced the data in the table for the number of bedrooms and house price. Is the price of the house independent of whether it has 3 or more bedrooms?
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We'll be doing a ChiSquare Test of Independence.
Null Hypothesis: The two variables "price" and "bedroom count" are independent. There's no connection between them. Changing one variable does not cause the other to change.
Alternative Hypothesis: The two variables "price" and "bedroom count" are dependent. There's a connection somehow. Changing one variable causes a change in the other.
Since the level of significance isn't stated, I'll assume the standard default of alpha = 0.05
Given Data
| 3 or More Bedrooms | | House Price | Yes | No | | Less than $300K | 344 | 499 | | $300-450K | 190 | 334 | | $450-600K | 133 | 293 |
Compute the row and column totals by adding the values.
Eg: 344+499 = 843 total houses are priced less than $300K
| 3 or More Bedrooms | | | House Price | Yes | No | Total | | Less than $300K | 344 | 499 | 843 | | $300-450K | 190 | 334 | 524 | | $450-600K | 133 | 293 | 426 | | Total | 667 | 1126 | 1793 |
The fact we get 1793 as the grand total helps act as a checksum of sorts.
The given data table represents the set of observed values. With ChiSquare problems, the letter O represents "observed values".
This is unfortunate since this letter looks a lot like the number zero.
The letter E represents expected values. To compute each expected value, we multiply the row and column totals, and then divide by the grand total N = 1793
For example, we expect the value 313.597881 in row1,column1 since:
E = (rowTotal*columnTotal)/N
E = (843*667)/1793
E = 313.59788064696
E = 313.597881
For more information and further examples, check out this page
https://online.stat.psu.edu/stat200/book/export/html/230
We'll follow that idea for the remaining other cells to get this set of expected values
| 3 or More Bedrooms | | House Price | Yes | No | | Less than $300K | 313.597881 | 529.402119 | | $300-450K | 194.929169 | 329.070831 | | $450-600K | 158.47295 | 267.52705 |
Once again:
O = observed value
E = expected value
We'll compute the value 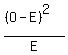 for each of the 6 cells for each of the 6 cells
Here's an example calculation for the item in row1,column1.
O = 344
E = 313.597881
 approximately. approximately.
Similar calculations will apply to the remaining five other cells
This is what that table of values looks like
| 3 or More Bedrooms | | House Price | Yes | No | | Less than $300K | 2.94737 | 1.745911 | | $300-450K | 0.124644 | 0.073834 | | $450-600K | 4.094523 | 2.425441 |
At this point we add up all of those values
2.94737+1.745911+0.124644+0.073834+4.094523+2.425441 = 11.411723
Therefore,
ChiSquare = 11.411723
This is the test statistic in which we'll compare to the critical value.
Now you'll refer to a ChiSquare table which is found in the appendix section of your stats textbook.
Check out this page for more info
https://www.statology.org/how-to-read-chi-square-distribution-table/
That page explains how to read a ChiSquare table.
In this case we have
r = 3 rows
c = 2 columns
df = degrees of freedom for a ChiSquare independence test
df = (r-1)*(c-1)
df = (3-1)*(2-1)
df = 2
Locate the df = 2 row
Then locate the column with header 0.05 to represent the alpha value
The value 5.991 is found here
What this means is that P(ChiSquare > 5.991) = 0.05 approximately when df = 2.
About 5% of the area is to the right of the critical value 5.991 when df = 2.
To recap we found that:
ChiSquare Test Statistic = 11.411723
ChiSquare Critical Value = 5.991
Keep in mind that ChiSquare tests are always right-tailed. This fact is mentioned in the first link I posted.
So this fact means that the rejection region is to the right of the critical value 5.991
The test statistic (11.411723) is greater than the critical value (5.991); therefore we are in the rejection region and we reject the null.
We reject the idea the variables are independent, so we conclude the price is dependent on the number of bedrooms. This makes sense. A bigger house should cost more. Of course there are other factors to consider such as location and the condition of the house, among other things.
Here are a few handy calculators to check your work:
https://www.mathsisfun.com/data/chi-square-calculator.html
https://www.statology.org/chi-square-test-of-independence-calculator/
https://www.gigacalculator.com/calculators/chi-square-calculator.php
-------------------------
Note: if the p-value is less than alpha = 0.05, then reject the null. Otherwise, you would fail to reject it (i.e. "accept" the null). In this case, the p-value is roughly 0.003326 which helps confirm why we reject the null.
Here's what the command looks like to compute the ChiSquare p-value on a TI83

To get to the command, press the key labeled "2nd" then press the VARS key. Scroll down to item 7.
If you don't have a TI83 or TI84 type calculator, then you can use one of the previous links mentioned earlier. Many more can be found by searching out "chi square calculator".
The command CHIDIST is used to compute ChiSquare p-values in spreadsheet programs like Excel.
Edit: Here's what it would look like using a spreadsheet. You don't need a Google account to access this Google Sheets document.
https://docs.google.com/spreadsheets/d/1CFeiCWPokyyataD6hwabsFZnCSMSxfTw08qwJvGq_R8/edit?usp=sharing
You can click on any cell to see what formulas were used.
|
|
|