Question 1196638: Real estate ads suggest that 52% of homes for sale have garages, 39% have swimming pools, and 10% have both features
a) What is the probability that a home for sale has a garage, but not a pool?
b) If a home for sale has a garage, what's the probability that it has a pool, too?
c) Are having a garage and having a pool independent events? Explain.
d) Are having a garage and having a pool mutually exclusive? Explain
Answer by ikleyn(52790)   (Show Source):
You can put this solution on YOUR website! .
Real estate ads suggest that 52% of homes for sale have garages, 39% have swimming pools, and 10% have both features
a) What is the probability that a home for sale has a garage, but not a pool?
b) If a home for sale has a garage, what's the probability that it has a pool, too?
c) Are having a garage and having a pool independent events? Explain.
d) Are having a garage and having a pool mutually exclusive? Explain
~~~~~~~~~~~~~~~~~
(a) P(a home has a garage, but not a pool) = P(has a garage) - P(have both) = 52% - 10% = 42%. ANSWER
(b) This question asks about the conditional probablity
P(a home has a pool given that it has a garage) = P(has a pool | has a garage) = 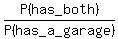 =  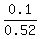=  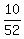. ANSWER
(d) Mutually exlusive means "no intersection", or "empty intersection".
Is the intersection empty in this problem ? - the answer is in the post.
(c) To check if these events are independent, you should compare the numbers
P(garage)*P(pool), from one side, and P(both), from the other side.
Using the given data in the post, calculate and compare.
If the numbers are the same, then the events are independent.
If the numbers are the different, then the events are NOT independent.
In (a) and (b), you have my answers with explanations.
In (c) and (d), you have all needed instructions.
|
|
|
