SOLUTION: Solve for all values of x in the interval [0, 2𝜋] that satisfy the equation. 4 sin(2x) = 4 cos(x)

4 sin(2x) = 4 cos(x)  implies, by canceling common factor "4" in both sides

    sin(2x) = cos(x),

    2sin(x)*cos(x) = cos(x)

    2sin(x)*cos(x) - cos(x) = 0

    cos(x)*(2sin(x) - 1) = 0


So, EITHER  cos(x) = 0,  OR  sin(x) = 1/2.


If cos(x) = 0,  then  x=   or  x= .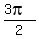


If sin(x) = 1/2,  then  x=   or  x=  -  = .


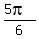So, the solution to the given equation are  ,  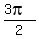,  ,  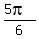.    ANSWER