Question 1196590: A boy is at a point A on a straight river. He can row downstream at a rate which is 2 miles an hour faster than he can run. If he rows downstream to a point B, which is 4 miles below A, and runs, in a direction perpendicular to the river, to a point C, three miles from B, it takes him ten minutes longer than it does to run directly from A to C. How fast can he run?
Answer by ikleyn(52754)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A boy is at a point A on a straight river.
He can row downstream at a rate which is 2 miles an hour faster than he can run.
If he rows downstream to a point B, which is 4 miles below A, and runs,
in a direction perpendicular to the river, to a point C, three miles from B,
it takes him ten minutes longer than it does to run directly from A to C.
How fast can he run?
~~~~~~~~~~~~~
Notice that ABC is a right angled triangle with right angle at B.
The hypotenuse AC is 5 miles long (the legs AB and BC are 4 miles and 3 miles, respectively).
Let x be his rate running, in miles per hour.
Then his rate rowing downstream is (x+2) miles, according to the problem.
His time running AC is 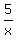 hours.
His time rowing from A to B and then running from B to C is hours.
His time rowing from A to B and then running from B to C is  + +  hours.
The time equation is hours.
The time equation is
 + + 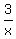 - - 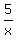 = 1/6 of an hour (i.e. 10 minutes). (1)
+------------------------------------------+
| At this point, the setup is complete. |
+------------------------------------------+
To solve equation, multiply both sides by 6x*(x+2). You will get
24x + 18(x+2) - 30(x+2) = x*(x+2)
24x + 18x + 36 - 30x - 60 = x^2 + 2x
12x - 24 = x^2 + 2x
x^2 - 10x + 24 = 0
(x-6)*(x-4) = 0
It gives two roots: x= 6 mph and x= 4 mph.
We keep both roots x = 6 mph and x = 4 mph as possible answers.
Let check by substituting this value into equation (1)
x = 6: = 1/6 of an hour (i.e. 10 minutes). (1)
+------------------------------------------+
| At this point, the setup is complete. |
+------------------------------------------+
To solve equation, multiply both sides by 6x*(x+2). You will get
24x + 18(x+2) - 30(x+2) = x*(x+2)
24x + 18x + 36 - 30x - 60 = x^2 + 2x
12x - 24 = x^2 + 2x
x^2 - 10x + 24 = 0
(x-6)*(x-4) = 0
It gives two roots: x= 6 mph and x= 4 mph.
We keep both roots x = 6 mph and x = 4 mph as possible answers.
Let check by substituting this value into equation (1)
x = 6:  + +  - -  = =  = =  = = 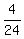 = =  (correct),
x = 4: (correct),
x = 4: 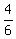 + +  - -  = =  = =  = =  = =  (correct).
ANSWER. There are two answers: the running speed can be 4 miles per hour and/or 6 miles per hour. (correct).
ANSWER. There are two answers: the running speed can be 4 miles per hour and/or 6 miles per hour.
Solved.
|
|
|