SOLUTION: The probability that an international flight leaving the United States is delayed in departing (event D) is .35. The probability that an international flight leaving the United Sta

You are given three facts :


    - The probability that an international flight leaving the United States is delayed in departing (event D) is 0.35.


    - The probability that an international flight leaving the United States is a transpacific flight (event P) is 0.40.


    - The probability that an international flight leaving the U.S. is a transpacific flight and is delayed in departing is .14.

          This event is the intersection of events D and P, so you are given the probability of intersection of these events

               p( D ∩ P ) = 0.14.


The problem's question asks about the conditional probability  P(D|P).


By the definition, for any two events P and D, the conditional probability  P(D|P) is this fraction

               p(D|P) = p ( D ∩ P ) / p(P).


Substitute the given data into this formula, and you will get


              p(D|P) = 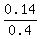 = 0.35.


It is your ANSWER :   The probability that an international flight leaving the United States is delayed in departing 
                      given that the flight is a transpacific flight is 0.35.

To answer this question, you should sheck if  p ( D ∩ P ) = p(D) * p(P).


Left  side is 0.14 (given).

Right side is 0.35*0.4 = 0.14.


Hence the events D and P are independent.