Question 1196548: Let g(x)=9x²-2. Find the average rate of change of the function as x changes from -8 to 5.
I don't know how to solve this. only tell me the steps for solving it
DON'T GIVE ME THE ANSWER!! just the steps, please. <(0U0)>
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
The average rate of change of a function f(x) as x changes from "a" to "b" on the number line, is the ratio
average rate of change =  .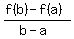
Step by step, it means that you calculate
(a) f(a);
(b) f(b);
(c) the difference f(b)-f(a) <<<--=== in this order (!)
(d) the difference (b-a) <<<---=== in this order (!)
(e) then divide the difference f(b)-f(a) by the difference (b-a).
Your question is answered and the procedure is described in full, step by step.
For more information, and to see many solved examples (your templates), look at numerous web-sites in the internet,
for example, this web-site
https://byjus.com/average-rate-of-change-formula/#:~:text=The%20Average%20Rate%20of%20Change,amount%20of%20change%20in%20another.
The keywords for such search are " average rate of a function ".
Come again to this forum soon to learn something new ( ! )
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Here's a similar example.
Question:
Let f(x) = x^2+7
Find the average rate of change from x = 3 to x = 5
Solution:
Plug in x = 3
f(3) = 3^2+7 = 9+7 = 16
Repeat for x = 5
f(5) = 5^2+7 = 25+7 = 32
These are the y values for the mentioned x inputs.
The two points (3,16) and (5,32) are on the function curve x^2+7
The task of finding the average rate of change is exactly the same as finding the slope of the line through those two points.
m = slope
m = rise/run
m = (change in y)/(change in x)
m = (y2-y1)/(x2-x1)
m = (32-16)/(5-3)
m = 16/2
m = 8
The slope of the line through (3,16) and (5,32) is 8, which is the average rate of change.
A real world application would be to look at the average speed of a car over some set amount of time.
Answer: 8
Keep in mind that this is of course just an example and not the answer to your question in particular.
However, you'll follow this same basic outline of steps.
|
|
|
