Question 1196475: A compact car can be rented from firm A for $160 per week with no charge for mileage or from firm B for $100 per week plus 20 cents for each mile driven. If the car is driven m miles, for what values of m does it cost less to rent from firm A?
Found 2 solutions by math_tutor2020, MathTherapy:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Edit: I realize I had the wrong final conclusion, but I have fixed the error. My apologies.
m = number of miles driven
c = cost for the week
firm A: c = 160
firm B: c = 0.20m+100
Equate the cost expressions and solve for m
0.20m+100 = 160
0.20m = 160-100
0.20m = 60
m = 60/0.20
m = 300
The two firms charge the same amount if you drove 300 miles for that week.
Anything larger than this will have firm B cost more.
Example: If you drive 400 miles, then firm B costs 0.20m+100 = 0.20*400+100 = 180 which is 20 dollars more than the $160 charged from firm A.
Answer: 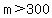
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A compact car can be rented from firm A for $160 per week with no charge for mileage or from firm B for $100 per week plus 20 cents for each mile driven. If the car is driven m miles, for what values of m does it cost less to rent from firm A?
Firm A's cost, with UNLIMITED miles: $160
Firm B's cost, with "m" miles driven: .2m + 100
We then get the following INEQUALITY: 160 < .2m + 100
Solve that to get m > 300, which means that, for Firm A to cost less than Firm B, one has to drive more than 300 miles.
|
|
|