Question 1196442: In a certain year, the probability that a person in the United States would declare personal bankruptcy was 0.004. The probability that a person in the United States would declare personal bankruptcy and had recently experienced a "big three" event (loss of job, medical problem, or divorce or separation) was 0.002. What was the probability that a person had recently experienced one of the "big three" events, given that she had declared personal bankruptcy? (Round your answer to four decimal places.)
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a certain year, the probability that a person in the United States would declare personal bankruptcy was 0.004.
The probability that a person in the United States would declare personal bankruptcy and had recently
experienced a "big three" event (loss of job, medical problem, or divorce or separation) was 0.002.
What was the probability that a person had recently experienced one of the "big three" events,
given that she had declared personal bankruptcy? (Round your answer to four decimal places.)
~~~~~~~~~~~~~~~~~~~~~~
Let A be an event that a person in the United States would declare personal bankruptcy.
Let B be an event that that a person in the United States had recently experienced a "big three" event
(loss of job, medical problem, or divorce or separation).
The problem wants you find a CONDITIONAL PROBABILITY of the event P(A and B) given A.
This probability is the ratio
P(A and B)/P(A) = 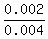 = =  = 0.5 = 50%. ANSWER = 0.5 = 50%. ANSWER
Solved and thoroughly explained.
|
|
|