|
Question 1196433: How many numbers between 10 and 1000 have a digit sum of 8?
Found 3 solutions by math_helper, greenestamps, ikleyn:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
44, found using this one-line perl script
perl -e '$c=0; for($i=10;$i<1001;$i++) { $s = "$i"; @c = split(//,"$s"); $sum=0; foreach( @c ) { $sum += $_;}; if ($sum == 8) { print "$i $sum\n"; } else { print "$i\n"; }}' | grep ' 8' | wc -l
44
To see the raw output of just the numbers that have digits adding to 8:
perl -e '$c=0; for($i=10;$i<1001;$i++) { $s = "$i"; @c = split(//,"$s"); $sum=0; foreach( @c ) { $sum += $_;}; if ($sum == 8) { print "$i $sum\n"; }}'
And to see ALL the numbers considered:
perl -e '$c=0; for($i=10;$i<1001;$i++) { $s = "$i"; @c = split(//,"$s"); $sum=0; foreach( @c ) { $sum += $_;}; if ($sum == 8) { print "$i $sum\n"; } else { print "$i\n"; }}'
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The numbers are either 2 or 3 digits. Logical analysis and observation of patterns makes it relatively easy to find the answer.
(1) 2-digit numbers
The first digit can be any digit from 1 to 8 (8 possibilities); for each first digit there is only one digit that makes a digit sum of 8.
ANSWER part 1: The number of 2-digit numbers with a digit sum of 8 is 8*1 = 8.
(2) 3-digit numbers
The first digit can be any digit from 1 to 8. For each of those digits, perform the analysis similar to that used for the 2-digit numbers.
1st digit 1: The sum of the other 2 digits must be 7, so the second digit can be any digit from 0 to 7. That's 8 possibilities.
1st digit 2: The sum of the other 2 digits must be 6, so the second digit can be any digit from 0 to 6. That's 7 possibilities.
You can do the detailed analysis for the other first digits if you want. But it should be clear that the numbers of 3-digit numbers with other first digits will decrease by 1 for each increase of 1 in the first digit.
ANSWER part 2: The number of 3-digit numbers with a digit sum of 8 is 8+7+...+2+1 = 36.
FINAL ANSWER: The number of numbers between 10 and 1000 with a digit sum of 8 is 8+36 = 44.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The meaning of the word " between " in Math problems is not precisely defined.
Every time you should explain, if endpoints are included or not.
So, I will re-formulate the problem in this form
+---------------------------------------------------------------------+
| How many numbers from 10 to 999 inclusive have a digit sum of 8? |
+---------------------------------------------------------------------+
Solution
For a minute, I will change my problem and ask
+-----------------------------------------------------------------------+
| How many numbers from 0 to 999 inclusive have a digit sum of 8? |
+-----------------------------------------------------------------------+
Then it is the same as to ask
How many integer solutions does this equation have
 + +  + +  = 8
in integer non-negative numbers = 8
in integer non-negative numbers  >= 0, >= 0,  >= 0, >= 0,  >= 0 ?
The answer is known from Combinatorics ( " Stars and Bars method " ),
( see this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)#:~:text=In%20the%20context%20of%20combinatorial,his%20classic%20book%20on%20probability. )
The number of solution in this case is >= 0 ?
The answer is known from Combinatorics ( " Stars and Bars method " ),
( see this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)#:~:text=In%20the%20context%20of%20combinatorial,his%20classic%20book%20on%20probability. )
The number of solution in this case is 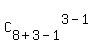 = =  = =  = 45.
From it, we should subtract 1, which represents the number "8",
(we included it, when extended the set from [10,999] to [0,999]).
After subtracting, we get the final
ANSWER. There are 45-1 = 44 integer numbers from 10 to 999 (inclusive), such that the sum of their digits is 8. = 45.
From it, we should subtract 1, which represents the number "8",
(we included it, when extended the set from [10,999] to [0,999]).
After subtracting, we get the final
ANSWER. There are 45-1 = 44 integer numbers from 10 to 999 (inclusive), such that the sum of their digits is 8.
Solved.
|
|
|
| |