Question 1196425: Suppose you are setting up a full-mesh network for x users; and n, the number of two-way connections required to link all users pairwise, must be no greater than 132. For what range of x values can you set up your network?
x(x-1)/2=n
Answer by ikleyn(52855)   (Show Source):
You can put this solution on YOUR website! .
Suppose you are setting up a full-mesh network for x users;
and n, the number of two-way connections required to link all users pairwise,
must be no greater than 132. For what range of x values can you set up your network?
x(x-1)/2=n
~~~~~~~~~~~~~~~~
They want you solve this inequality
 <= 132
in positive integer numbers.
So, you multiply both sides by 2
x*(x-1) <= 2*132 = 264.
At this point, you can estimate x by noticing that  = 16.24... (rounded.
Hence, integer x must be closest to it lesser integer  .
CHECK. 16*(16-1) = 16*15 = 240, while 17*16 = 272, confirming this answer.
Alternatively, you can solve quadratic inequality
x^2 - x - 264 <= 0,
and for x you will get
 =  =  =  .
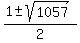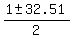Thus -15.755 <= x <= 16.755, and since we want x be positive integer number, it gives the same answer x <= 16.
Solved in two ways for your better understanding, giving the ANSWER n <= 16.
|
|
|
