Question 1196416: A ball is thrown across a playing field from a height of 5 ft above the ground at an angle of 45 degrees to the horizontal at a speed of 20ft/s. It can be deduced from physical principles that the height of the ball is modeled by the function,
h(x)=-32/(20)^2x^2+x+5
where x is the distance in feet that the ball has traveled horizontally.
(1) If the ball traveled horizontally 10 ft, what is the height?
(2) Find the maximum height obtained by the ball. (enter two decimals points).
(3) Find the horizontal distance the ball has traveled when it hits the ground. (enter two decimal points).
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!  ..........simplify ..........simplify


(1) If the ball traveled horizontally 10ft, what is the height?



If the ball traveled horizontally 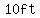 , the height is , the height is  . .
(2) Find the maximum height attained by the ball. (Round your answer to three decimal places.)
This is plainly a parabolic function - it fits the form  . Since a is negative, it is an inverted parabola, one whose opening points downwards. Such a parabola has a maximum value, which in this case corresponds to the maximum height reached by the ball. . Since a is negative, it is an inverted parabola, one whose opening points downwards. Such a parabola has a maximum value, which in this case corresponds to the maximum height reached by the ball.
The maximum or minimum value of a parabola occurs at the  , which itself is located at the , which itself is located at the  coordinate of coordinate of 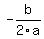 , based on our standard form. , based on our standard form.
With  and an and an  we have we have

this corresponds to 
We find the height the ball reaches at this point by plugging the  into our equation. into our equation.
 . .
The maximum height attained by the ball is 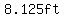 . .
(3)
Find the horizontal distance the ball has traveled when it hits the ground. (Round your answer to one decimal place.)
The horizontal distance covered corresponds to the x value where the ball reaches a height of  . I.e., it's one of the roots of the function, which can be found with the quadratic equation, . I.e., it's one of the roots of the function, which can be found with the quadratic equation,

Plugging in our coefficients, we have





There is one positive solution and one negative solution to this - for physical reasons, the 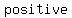  is the one we prefer, since we're looking for where the ball hits the ground ahead of the thrower. is the one we prefer, since we're looking for where the ball hits the ground ahead of the thrower.
Thus, our answer is


the horizontal distance the ball has traveled when it hits the ground is 
|
|
|