Question 1196361: The Opposite Flying Plane Problem: Two planes flying opposite directions (North and South) pass each other 80 miles apart at the same altitude. The Northbound plane is flying 200 mph and the Southbound plane is flying 150 mph. a) How far apart are the planes in 20 minutes? b) When are the planes 300 miles apart?
Found 2 solutions by math_tutor2020, MathTherapy:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!
Part (a)
Let's label the planes as PlaneA and PlaneB
PlaneA = northbound at 200 mph
PlaneB = southbound at 150 mph
Place planeA at (0,0) on the xy grid.
PlaneB will go to (80,0) which is 80 units away, to represent the 80 mile gap.
t = number of hours that elapse, after the planes are side by side
The location of planeA is (0,200t) since it travels 200 mph and it's heading north, i.e. along the positive y axis.
I'm using the idea that distance = rate*time
For instance, after t = 1 hour, plane A is at location (0,200t) = (0,200*1) = (0,200)
Meanwhile, the location of planeB is (80,-150t)
The negative is to indicate going south
20 min = 20/60 = 1/3 of an hour
Let's plug in t = 1/3 to find the location of each plane
A = (0,200t) = (0,200*(1/3)) = (0,200/3)
B = (80,-150t) = (80,-150*(1/3)) = (80,-50)
Now compute the distance from A to B
d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
d = sqrt( (0-80)^2 + (200/3-(-50))^2 )
d = sqrt( (0-80)^2 + (200/3+50)^2 )
d = sqrt( 20,011.1111111111 )
d = 141.46063449282
d = 141.4606
Answer: Approximately 141.4606 miles
Round this however your teacher instructs.
=====================================================================================
Part (b)
Let's go back to
A = (0,200t)
B = (80,-150t)
and compute the distance based on these coordinates
d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
d = sqrt( (0-80)^2 + (200t-(-150t))^2 )
d = sqrt( 6400 + (200t+150t)^2 )
d = sqrt( 6400 + (350t)^2 )
d = sqrt( 6400 + 122,500t^2 )
As a slight detour, let's plug in t = 1/3 to get...
d = sqrt( 6400 + 122,500t^2 )
d = sqrt( 6400 + 122,500(1/3)^2 )
d = 141.46063449282
We get the same result as before, so it helps confirm we have the correct general distance equation.
What we'll do from here is plug in d = 300 and solve for t
d = sqrt( 6400 + 122,500t^2 )
300 = sqrt( 6400 + 122,500t^2 )
300^2 = 6400 + 122,500t^2
90,000 = 6400 + 122,500t^2
6400 + 122,500t^2 = 90,000
122,500t^2 = 90,000
122,500t^2 = 90,000 - 6400
122,500t^2 = 83,600
t^2 = (83,600)/(122,500)
t^2 = 0.68244897959183
t = sqrt(0.68244897959183)
t = 0.82610470256006
The planes are 300 miles apart at the time marker of approximately 0.82610470256006 hours
Multiply by 60 to convert to minutes
60*0.82610470256006 = 49.5662821536037
Answer: Approximately 49.5663 minutes
Round this value however your teacher instructs.
Answer by MathTherapy(10551)  (Show Source):
You can put this solution on YOUR website! The Opposite Flying Plane Problem: Two planes flying opposite directions (North and South) pass each other 80 miles apart at the same altitude. The Northbound plane is flying 200 mph and the Southbound plane is flying 150 mph. a) How far apart are the planes in 20 minutes? b) When are the planes 300 miles apart?
This scenario is best illustrated, much easier to undertstand and to follow, using a diagram.
When the planes pass each other they're 80 miles apart
Twenty minutes after passing each other, the Northbound covered:  , while the Southbound
covered: 
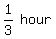Twenty minutes ( ) after passimg each other, a right triangle is formed by the planes, with the shorter leg being
80 miles and the longer leg,  .
The distance between them (hypotenuse of the right triangle, so formed) is: 
Now, after passing each other and the planes are 300 miles apart, another right triangle is formed, with the shorter leg being 80 miles
and the hypotenuse, 300 miles. The longer leg is then: 
However, the longer leg consists of the following segments:
1) 150T miles (the distance the Southbound travelled to get to 300 miles of the Northbound, with T being the
time the Southbound took to travel from the point where they were 20 minutes after passimg each other, to the point
where they were 300 miles apart)
2) 50 miles (the distance covered by the Southbound, 20 minutes after they passed each other)
3)  miles (the distance covered by the Northbound, 20 minutes after they passed each other)
4) 200T miles (the distance the Northbound travelled to get to 300 miles of the Southbound, with T being the time the Northbound took to
travel from the point where they were 20 minutes after passimg each other, to the point where they were 300 miles apart)
This gives us: 
Finally, time they each took to travel from the point where they were 20 minutes after passimg each other, to the point where they
were 300 miles apart, or 
OR
Time they each took to travel from the point where they passed each other, to the point where they were 300 miles
apart: 20 + 29.56686 = 49.56686 minutes
|
|
|
