Question 1196346: Hello, can anybody explain this problem to me? Thanks:
Let f be a one-to-one function and c be a real number. State an expression for
the inverse of g(x) = f (x + c) in terms of f^−1, and prove that your formula is correct.
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hello, can anybody explain this problem to me? Thanks:
Let f be a one-to-one function and c be a real number. State an expression for
the inverse of g(x) = f (x + c) in terms of f^−1, and prove that your formula is correct.
~~~~~~~~~~~~~~~~~~~~
We are given two functions, f(x) and g(x) = f(x+c), which map the set of real numbers R
one-to-one in R. We express it by using this diagram with these standard symbols of mapping
f, g : 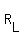 ---> ---> 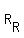 (1)
{x} {y}
For more expressiveness, we use variable x for real numbers of the left side R = (1)
{x} {y}
For more expressiveness, we use variable x for real numbers of the left side R = 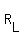 and use variable y for real numbers of the right side R =
and use variable y for real numbers of the right side R = 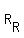 , as shown in the formula (1).
So we write expressions like these
y = f(x), y = g(x).
Couple of useful notes
(1) According to the problem's context, functions f and g are defined over entire R.
(2) The image of f is the same as the image of g.
I don't want to spend time, words and place for explaining it;
it should be clear for the reader, whose level is adequate to the problem.
+-------------------------------------------------------------------------------------------+
| The problem asks to express , as shown in the formula (1).
So we write expressions like these
y = f(x), y = g(x).
Couple of useful notes
(1) According to the problem's context, functions f and g are defined over entire R.
(2) The image of f is the same as the image of g.
I don't want to spend time, words and place for explaining it;
it should be clear for the reader, whose level is adequate to the problem.
+-------------------------------------------------------------------------------------------+
| The problem asks to express 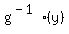 in terms of in terms of  . |
| |
| Notice that this requirement does not specify, which argument of . |
| |
| Notice that this requirement does not specify, which argument of  to use. |
| |
| This uncertainty OPENS the way to move forward. |
+-------------------------------------------------------------------------------------------+
Let y belongs to the image of g (which is the same as the image of f).
By the definition of the inverse function, to use. |
| |
| This uncertainty OPENS the way to move forward. |
+-------------------------------------------------------------------------------------------+
Let y belongs to the image of g (which is the same as the image of f).
By the definition of the inverse function,
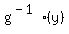 = =  , (2)
where x is the unique real number (in the left side R of (1)), such that g(x) = y.
Next, we know that , (2)
where x is the unique real number (in the left side R of (1)), such that g(x) = y.
Next, we know that 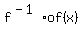 = x (the composition of f and = x (the composition of f and  is the identical map).
Therefore, we can re-write formula (2) in this way is the identical map).
Therefore, we can re-write formula (2) in this way
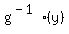 = = 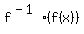 , (3)
where x is the unique real number (in the left side R of (1)), such that g(x) = y.
You may consider (3) as the desired expression for , (3)
where x is the unique real number (in the left side R of (1)), such that g(x) = y.
You may consider (3) as the desired expression for 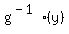 ,
or very close to it.
Or, if you want to have an analog of (3), where all the parts and all the terms of
the right side are expressed in terms of f(x) only, you can replace g(x) = y by f(x-c) = y.
Then your final answer will sound this way ,
or very close to it.
Or, if you want to have an analog of (3), where all the parts and all the terms of
the right side are expressed in terms of f(x) only, you can replace g(x) = y by f(x-c) = y.
Then your final answer will sound this way
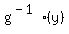 = = 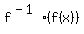 , (4)
or this way , (4)
or this way
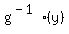 = = 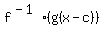 , (5)
where x is the unique real number (in the left side R of (1)), such that f(x-c) = y. , (5)
where x is the unique real number (in the left side R of (1)), such that f(x-c) = y.
At this point, the solution is complete.
/////////////////
I understand that for beginner reader this reasoning may seem hard,
but you receive what you request exactly as is.
To understand it in full, you need read it very attentively,
think on each word and each sentence and use diagrams.
If you have question, do not hesitate to ask.
At which school / college / university / thinking center
did you receive this problem ?
------------------------
Comment from student: Thanks for helping me out! To respond to your question,
this is a problem from the hw for Umtymp Calc, the youth math program at U of M.
My response. I got your message as a comment. Thanks for it.
I am proud by myself, too . . .
In the Internet, I found the info about this program and this school,
and I place it here - - - for memory.
About UMTYMP
https://cse.umn.edu/mathcep/about-umtymp
The University of Minnesota Talented Youth Mathematics Program (UMTYMP)
has been one of the nation's premier accelerated programs for students
who are highly talented in mathematics over the last forty years.
UMTYMP is unique in terms of the number of students, length of the program,
scope of the curriculum, and the number of University of Minnesota credits
granted to students in middle school and high school.
Come again to this forum soon to learn something new ( ! )
|
|
|