Question 1196331: The Marketing Executive Problem: A marketing executive traveled 810 miles on a corporate jet in the same amount of time that it took to travel 162 mi by helicopter. The rate of the jet was 360 mph greater than the rate of the helicopter. Find the rate of the jet.
Found 3 solutions by ikleyn, amoresroy, greenestamps:
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website! .
The Marketing Executive Problem: A marketing executive traveled 810 miles on a corporate jet in the same amount
of time that it took to travel 162 mi by helicopter. The rate of the jet was 360 mph greater than the rate of
the helicopter. Find the rate of the jet.
~~~~~~~~~~~~~~~~~~~~~~
Start writing "time" equation as you read the problem
 = 
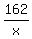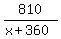Cross multiply, then simplify
162(x+360) = 810x
162x + 58320 = 810x
58320 = 810x - 162x
58320 = 648x
x = 58320/648 = 90.
Thus the helicopter's rate is 90 miles per hour.
Then the jet's rate is 90 + 360 = 450 miles per hour. ANSWER
Solved.
Answer by amoresroy(361)  (Show Source):
You can put this solution on YOUR website! Let x = the speed rate of the helicopter in mph
x + 360 = the speed rate of the jet in mph
Travel time is calculated as distance traveled divided by speed rate
810/(x+30) = time traveled by jet
162/x = time traveled by helicopter
So we have the following equation:
810/(x+360) = 162/x
Solve for x
810(x) = 162(x+360)
810x = 162x + 58,320
810x - 162x = 58,320
648x = 58,320
x = 58,320/648
x = 90
x + 360 = 450 (speed of the jet
Answer:
The speed rate of the jet is 450 mph.
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The distances are 810 and 162 miles, and the times are the same, so the ratio of the two speeds is the same as the ratio of the distances -- 810:162 = 5:1.
Knowing that ratio, let the speed of the jet be 5x and the speed of the helicopter x. The difference between the two speeds is then 4x.
But the difference in the two speeds is 360mph; so 4x = 360 and x = 90.
So the speed of the helicopter is x = 90mph and the speed of the jet is 5x = 450mph.
ANSWER: 450mph
|
|
|
