Question 1196288: Olivia bought four composition notebooks and three packs of pencils from the school bookstore and paid $10.93. Jackie bought seven composition notebooks and two packs of pencils and paid $13.31. What is the price of a pack of pencils? (Do not include the $ in your answer).
Found 4 solutions by ikleyn, MathLover1, MathTherapy, greenestamps:
Answer by ikleyn(52833)   (Show Source):
You can put this solution on YOUR website! .
Olivia bought four composition notebooks and three packs of pencils
from the school bookstore and paid $10.93.
Jackie bought seven composition notebooks and two packs of pencils
and paid $13.31.
What is the price of a pack of pencils? (Do not include the $ in your answer).
~~~~~~~~~~~~~~~
Solve using the determinant method.
Equations:
4N + 3P = 10.93
7N + 2P = 13.31
----------------------
P = 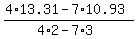 = 1.79.
ANSWER. A pack of pencils costs 1.79 dollars.
Solved.
For such problems, the determinant methos is fastest and most straighforward way to get the answer.
---------------
On the Determinants' method for solving systems of two linear equations in two unknowns see the lesson
- Solution of the linear system of two equations in two unknowns using determinant
in this site.
Answer by MathLover1(20850)  (Show Source):
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website!
Olivia bought four composition notebooks and three packs of pencils from the school bookstore and paid $10.93. Jackie bought seven composition notebooks and two packs of pencils and paid $13.31. What is the price of a pack of pencils? (Do not include the $ in your answer).
DO NOT bother to even look at that woman's RIDICULOUS method of solving this. It's as usual, complicated as HELL,
with all those solutions of variables that form UNNECESSARY fractions that take forever and leaves one prone to
multiple mistakes!! She needs to learn mathematics!
Let cost of a pack of pencils, and each notebook, be P and N, respectively
Then we get: 4N + 3P = 10.93 ----- eq (i)
Also, 7N + 2P = 13.31 ----- eq (ii)
3N - P = 2.38 ------ Subtracting eq (i) from eq (ii) ----- eq (iii)
N + 4P = 8.55 ------ Subtracting eq (iii) from eq (i) =====> N = 8.55 - 4P ----- eq (iv)
3(8.55 - 4P) - P = 2.38 ------ Substituting 8.55 - 4P for N in eq (iii)
25.65 - 12P - P = 2.38
- 13P = 2.38 - 25.65
- 13P = - 23.27
Cost of a pack of pencils or 
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
When the two given equations are both in standard form Ax+By=C, my preference for an algebraic method for solving the problem is elimination.
4x+3y = 10.93
7x+2y = 13.31
Multiply the first equation by 2 and the second by -3 and add the two resulting equations; that will eliminate y:
8x+6y = 21.86
-21x-6y = -39.93
----------------
-13x = -18.07
x = 18.07/13 = 1.39
Then use that in either of the original equations to find y.
4(1.39)+3y = 10.93
5.56+3y = 10.93
3y = 5.37
y = 5.37/3 = 1.79
ANSWER: The cost of a pack of pencils is $1.79
(Note that, since the problem asks only for the cost of a pack of pencils, I could have solved directly for y by eliminating x; I chose to eliminate y and then solve for y because it keeps the numbers smaller....)
|
|
|
