Question 1196229: Lotteries The Sad State Lottery requires you to select a sequence of four different numbers from 0 through 68. (Order is important.) You are a Winner if your sequence agrees with that in the drawing, and you are a Booby Prize Winner if your selection of numbers is correct, but in the wrong order. What is the probability of being a Winner? (Enter your probabilities as fractions.)
What is the probability of being a Booby Prize Winner?
What is the probability that you are either a Winner or a Booby Prize Winner?
Answer by ikleyn(52908)   (Show Source): (Show Source):
You can put this solution on YOUR website! Lotteries The Sad State Lottery requires you to select a sequence of four different numbers
from 0 through 68. (Order is important.)
You are a Winner if your sequence agrees with that in the drawing,
and you are a Booby Prize Winner if your selection of numbers is correct, but in the wrong order.
(a) What is the probability of being a Winner? (Enter your probabilities as fractions.)
(b) What is the probability of being a Booby Prize Winner?
(c) What is the probability that you are either a Winner or a Booby Prize Winner?
~~~~~~~~~~~~~~~~~~
(a) In all, there are 69 numbers, from which the organizers of the lottery select 4 numbers.
There are 69*68*67*66 = 20748024 different ORDERED sequences of 4 numbers from 69 numbers,
that you may have on your ticket, so the number of tickets in the lottery is 20748024,
and only one of them is a Winner.
Therefore, the probability to be a Winner, having one ticket, is P = 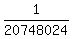 . ANSWER to (a)
(b) The number of "happy" tickets for to be a Booby Prize Winner is 4! -1 = 1*2*3*4 - 1 = 24 - 1 = 23
(permutations of 4 happy numbers minus one Winner ticket)
Therefore, the probability to be a Booby Prize Winner, having one ticket, is
P = . ANSWER to (a)
(b) The number of "happy" tickets for to be a Booby Prize Winner is 4! -1 = 1*2*3*4 - 1 = 24 - 1 = 23
(permutations of 4 happy numbers minus one Winner ticket)
Therefore, the probability to be a Booby Prize Winner, having one ticket, is
P =  = = 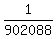 . ANSWER to (b)
(c) The probability to be either-or in this case is . ANSWER to (b)
(c) The probability to be either-or in this case is 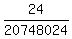 = = 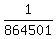 . ANSWER to (c) . ANSWER to (c)
Solved.
|
|
|