Question 1196201:
Suppose x is a positive number such that  . There is a unique choice of whole numbers p and q so that . There is a unique choice of whole numbers p and q so that  . Find p+q.
My attempt:
I know that if . Find p+q.
My attempt:
I know that if  , then , then  , which simplifies to , which simplifies to 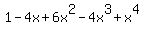 . Then what? . Then what?
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is VERY nice problem, admitting BEATIFUL solution.
See below.
If x^2 = 1-x, then
x^8 = (1-x)^4 = 1 - 4x + 6x^2 - 4x^3 + x^4.
The idea is to replace in this expression, and in all expressions that follow, x^2 by (1-x)
everywhere, where it is possible, and as many times as possible, until you get the desired
expression of degree 1 (one).
See how it works
x^8 = 1 - 4x + [6(1-x)] - [4x*(1-x)] + [(1-x)*(1-x)] = I continue =
= 1 - 4x + 6 - 6x - 4x + 4x^2 + 1 - 2x + x^2 = 8 - 14x + 5x^2 = I replace x^2 by (1-x) again =
= 8 - 14x + 5*(1-x) = 8 - 16x + 5 - 5x = 13 - 21x.
So, p = 13, q = 21 and p + q = 13 + 21 = 34. ANSWER
Solved.
This method is called " the lowering of a degree " method.
//////////////
It can be solved by different methods, but this one is a " true delight ".
Answer by MathTherapy(10556)   (Show Source): (Show Source):
|
|
|