Question 1196200: g is a trigonometric function of the form g(x)=a sin(bx+c)+d. Below is the graph g(x). The function intersects its midline at (pi/2,3.5) and has a minimum point at (-pi/2, -2). Find a formula for g(x). Give an exact expression.
Answer by greenestamps(13209)   (Show Source):
You can put this solution on YOUR website!
You don't show the graph; you only define it by one minimum point and one point of intersection with the midline. That leaves an infinite number of possible sine functions -- depending on how many cycles the graph has completed between the given minimum point and the given point of intersection with the midline.
I will assume that the given point of intersection with the midline is the first such intersection to the right of the given minimum point.
I will also use the more useful form of the function,  , in which the "c" is exactly the phase shift.
The change in x from a minimum point to the first intersection with the midline is 1/4 of a period; since that change is pi, the period of the function is 4pi. That makes b = 2pi/4pi = 1/2.
And since the basic sine graph is at the midline at x=0, and the intersection of the midline in this problem is x=pi/2, the phase shift is pi/2.
Finally, the given y values at the minimum and midline give us a=5.5 and d=3.5.
So one function with a graph containing the two given points is
Here is a graph of that function, along with the constant functions y=-2 and y=3.5.
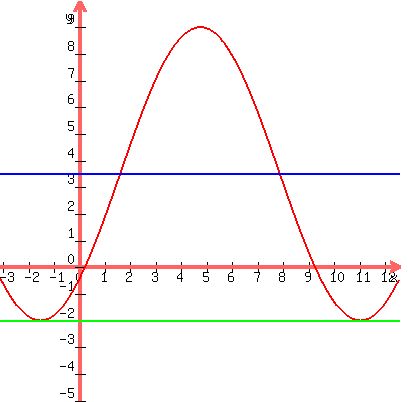
To demonstrate that there are other sine functions with graph containing the two given points, we can assume the case in which the intersection of the graph with the midline is the second one to the right of the minimum instead of the first.
In that case, the function has completed 3/4 of a cycle with a change of pi in the x value; that makes the period (4/3)pi, so b is 2pi/((4/3)pi) = (3/2)pi.
To determine the phase shift, the x coordinate of the first intersection to the right of the given minimum is now 1/3 of the way from the minimum at x=-pi/2 and the second intersection at pi/2. That makes the x coordinate of the first point of intersection with the midline (-1/6)pi.
So another sine function with a graph containing the two given points is
Here is the graph of this function, added to the previous graph:
The graph shows both sine functions passing through the given points (-pi/2,-2) and (pi/2,3.5)
And similarly there are an infinite number of other sine functions whose graphs contain those two points.
|
|
|
