Question 1196181: There are 15 green apples and 72 red apples in a basket. We keep extracting the apples randomly, one at a time, until we have extracted all 72red apples. What is the probability that the basket is empty when we finish?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13203)   (Show Source): (Show Source):
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are 15 green apples and 72 red apples in a basket.
We keep extracting the apples randomly, one at a time,
until we have extracted all 72 red apples.
What is the probability that the basket is empty when we finish?
~~~~~~~~~~~~~~
The solution by @greenestamps does not correspond to the posed question.
It does not correspond, becouse he considers the strings of the length 72+15 = 87, ONLY.
Meanwhile, the process can stop at any number of apples extracted between 72 and 87;
the only two conditions are that all 72 red apples are extracted and the last extracted apple is red.
The green apples can still remain in the basket when the process stops.
So, I came to bring another solution.
So, all possible outcomes are the strings of the length between 72 and 87 inclusive,
that contain 72 "R" and such that "R" is in the last position.
Let's consider only distinguishable arrangements.
The number of such strings of the length 72 is 1.
The number of such strings of the length 73 is 72 (a unique green apple is in any position from 1 to 72).
The number of such strings of the length 74 is  (two green apples are in any two positions from 1 to 73).
The number of such strings of the length 75 is (two green apples are in any two positions from 1 to 73).
The number of such strings of the length 75 is  (three green apples are in any three positions from 1 to 74).
By continuing this logical reasoning, the total number of all possible outcomes is the sum
Total = 1 + (three green apples are in any three positions from 1 to 74).
By continuing this logical reasoning, the total number of all possible outcomes is the sum
Total = 1 + 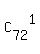 + +  + +  + . . . + + . . . +  + + 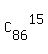 .
The favorable outcomes are the strings of the length 87 (that contain all the apples) with the red apple in the last position.
The number of such strings is Favorable = .
The favorable outcomes are the strings of the length 87 (that contain all the apples) with the red apple in the last position.
The number of such strings is Favorable = 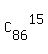 .
Now we should calculate these numbers.
To make it, I used Excel spreadsheet. It gave me Total = 26322377293583700; Favorable = 21784036380896900.
Now the ANSWER to the problem's question is this ratio
P = .
Now we should calculate these numbers.
To make it, I used Excel spreadsheet. It gave me Total = 26322377293583700; Favorable = 21784036380896900.
Now the ANSWER to the problem's question is this ratio
P = 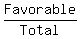 = = 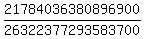 = 0.8276 (rounded). = 0.8276 (rounded).
Solved.
--------------
Again, @greenestamps answered other question, different from the posed in the problem, namely
"What is the probability that last extracted apple is red given that the basket is empty?"
although the real question in the problem is
"What is the probability that the basket is empty when we extract the 72-th red apple?"
The questions seems to be similar, but in reality they are different, and the logic of solutions is different.
===============
At the finish, I have even more interesting message to you.
When I calculated the probability according to the @greenestamps solution,
I got practically the same decimal rounded number of 0.8276.
The difference is in further decimal places.
So, numerically our answers are very close, but logically the solutions are different.
|
|
|