Question 1196129: Margin of Profit The margin of profit of a company is the net income divided by the total sales. A company's margin of profit increased by 0.02 from last year. Last year the company sold its product at $3.00 each and had a net income of $4500. This year it increased the price of its product by $0.50 each, sold 2000 more, and had a net income of $7140. The company never has had a margin of profit greater than 0.15. How many of its product were sold last year and how many were sold this year?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52754)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Margin of Profit
The margin of profit of a company is the net income divided by the total sales.
[1] A company's margin of profit increased by 0.02 from last year.
[2] Last year the company sold its product at $3.00 each and had a net income of $4500.
[3] This year it increased the price of its product by $0.50 each, sold 2000 more,
and had a net income of $7140.
[4] The company never has had a margin of profit greater than 0.15.
How many of its product were sold last year and how many were sold this year?
~~~~~~~~~~~~~~~~~~~~
I numbered the sentences for easy referring.
Let x be the number of their product that were sold last year.
From [2], we have this expression for margin profit last year
 , or , or  . (1)
From [3], we have this expression for margin profit this year . (1)
From [3], we have this expression for margin profit this year
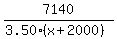 , or , or 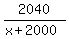 (2)
From [1], quantity (2) is 0.02 greater than quantity (1). It gives this equation (2)
From [1], quantity (2) is 0.02 greater than quantity (1). It gives this equation
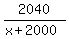 - -  = 0.02.
+-------------------------------------------------------------------+
| In this problem, the MAJOR STEP is to get a setup equation, |
| and we successfully overcome it (!) |
+-------------------------------------------------------------------+
+---------------------------------------+
| To solve it is just a brute force. |
+---------------------------------------+
Multiply both sides by x*(x+2000)
2040x - 1500(x + 2000) = 0.02x*(x+2000)
Simplify step by step
2040x - 1500x - 3000000 = 0.02x^2 + 40x
x^2 + 500x - 3000000 = 0
(x-1500)*(x+2000) = 0
So, the rots are 1500 and -2000. We reject the negative root,
and accept the positive one x= 1500.
Thus last year the company sold 1500 units of the product.
This year they sold 2000 units more, i.e. 1500 + 2000 = 3500 units of the product. = 0.02.
+-------------------------------------------------------------------+
| In this problem, the MAJOR STEP is to get a setup equation, |
| and we successfully overcome it (!) |
+-------------------------------------------------------------------+
+---------------------------------------+
| To solve it is just a brute force. |
+---------------------------------------+
Multiply both sides by x*(x+2000)
2040x - 1500(x + 2000) = 0.02x*(x+2000)
Simplify step by step
2040x - 1500x - 3000000 = 0.02x^2 + 40x
x^2 + 500x - 3000000 = 0
(x-1500)*(x+2000) = 0
So, the rots are 1500 and -2000. We reject the negative root,
and accept the positive one x= 1500.
Thus last year the company sold 1500 units of the product.
This year they sold 2000 units more, i.e. 1500 + 2000 = 3500 units of the product.
Solved.
I'd say it is a good problem of a university Olympiad level for students of Finance department (without any joke).
==============
Thanks to tutor @math_tutor2020 for correcting me !
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The tutor @ikleyn has the right idea, but made an error when going from
2040x - 1500x - 3,000,000 = 0.02x^2 + 40x
to
x^2 + 500x - 3,000,000 = 0
This is how I would continue the steps to solve for x
2040x - 1500x - 3,000,000 = 0.02x^2 + 40x
2040x - 1500x - 3,000,000 - 0.02x^2 - 40x = 0
-0.02x^2 + 500x - 3,000,000 = 0
Now apply the quadratic formula with
a = -0.02
b = 500
c = -3,000,000




 or or 
 or or 
 or or 
The two potential answers are
x = 10,000
x = 15,000
However we need to check them both
Let's check x = 10,000 first
If 10,000 units were sold last year, at $3 each, then the company earns 3*10,000 = 30,000 dollars in sales
Divide the net income for last year (4500) over the sales (30,000) and we'll get the profit margin for last year
margin = (4500)/(30,000) = 0.15
The profit margin for last year is 0.15, ie 15% of sales is net income
However, we've hit the ceiling since it states "The company never has had a margin of profit greater than 0.15"
So there's no way to have a profit margin increase of 0.02 to get to 0.15+0.02 = 0.17 for this current year.
Therefore, the value x = 10,000 is not a solution.
Now check x = 15,000
last year's sales = 15,000*3 = 45,000
last year profit margin = (net income)/(sales) = 4500/(45,000) = 0.10
The profit margin for last year was 0.10
So far so good since we're not at the ceiling of 0.15
this year's sales = (15,000+2,000)*(3+0.50) = 17,000*3.50 = 59,500
this years profit margin = (7140)/(59500) = 0.12 which is 0.02 more than 0.10
This confirms that x = 15,000 works as a solution
Answers:
15,000 units sold last year
17,000 units sold this year
|
|
|