Question 1196016: If a simple discount rate of 11% is equivalent to a simple interest rate of 14.5%. Then what is the length of time under consideration?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If a simple discount rate of 11% is equivalent to a simple interest rate of 14.5%.
Then what is the length of time under consideration?
~~~~~~~~~~~~~~~~~~~
In this problem, the most difficult part is to understand what they want from you.
I will explain it to you in full details.
Let B is the borrowed amount, and let R be the amount which should be returned.
Since the simple discount rate is 11%, we have this equation (the definitionm of the simple discount rate)
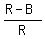 = 0.11,
which gives
R - B = 0.11*R, or B = R - 0.11R, or B = 0.89R. (1)
Next, since the loan is simple interest rate of 14.5%, the amount to return at the end is
R = B + 0.145*B*t, (2)
where t is the time in years, which is the unknown quantity in this problem.
Substitute B from equation (1) into equation (2). You will get
R = 0.89R + 0.145*(0.89*R)*t.
Cancel the factor R in both sides
1 = 0.89 + 0.145*0.89*t.
Simplify and find t
1 - 0.89 = 0.12905*t, or 0.11 = 0.12905*t, or t = = 0.11,
which gives
R - B = 0.11*R, or B = R - 0.11R, or B = 0.89R. (1)
Next, since the loan is simple interest rate of 14.5%, the amount to return at the end is
R = B + 0.145*B*t, (2)
where t is the time in years, which is the unknown quantity in this problem.
Substitute B from equation (1) into equation (2). You will get
R = 0.89R + 0.145*(0.89*R)*t.
Cancel the factor R in both sides
1 = 0.89 + 0.145*0.89*t.
Simplify and find t
1 - 0.89 = 0.12905*t, or 0.11 = 0.12905*t, or t = 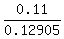 = 0.852383 of an year,
which is 0.852383*365 = 311.11 days, which we should round to 311 days.
ANSWER. The length of the time under consideration is 311 days (rounded). = 0.852383 of an year,
which is 0.852383*365 = 311.11 days, which we should round to 311 days.
ANSWER. The length of the time under consideration is 311 days (rounded).
Solved.
------------------
The "solution" by @josgarithmetic is incorrect, illogical and irrelevant.
You better ignore it, for the safety of your mind.
|
|
|