Question 1196010: Write an equation for a rational function with the given characteristics.
Vertical asymptotes at x = −4 and x = 8, x-intercepts at (−2, 0) and (1, 0),horizontal asymptote at y = −2
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Write an  expression for a rational function with the given characteristics. expression for a rational function with the given characteristics.
Vertical asymptotes at x = −4 and x = 8, x-intercepts at (−2, 0) and (1, 0),
horizontal asymptote at y = −2
~~~~~~~~~~~~~~~
A rational function R(x) is the ratio R(x) = 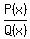 of two polynomials P(x) and Q(x).
We want the denominator Q(x) would have the zeroes at x= -4 and x= 8, giving
vertical asymptotes.
So we take Q(x) as a quadratic function Q(x) = (x-(-4))*(x-8) = (x+4)*(x-8).
Next we want the numerator P(x) would be zero at x= -2 and x= 1, providing
assigned x-intersectios. So we take the numersator P(x) as a quadratic function
P(x) = a*(x-(-2))*(x-1) = a*(x+2)*(x-1).
Now the ratio of two polynomials P(x) and Q(x).
We want the denominator Q(x) would have the zeroes at x= -4 and x= 8, giving
vertical asymptotes.
So we take Q(x) as a quadratic function Q(x) = (x-(-4))*(x-8) = (x+4)*(x-8).
Next we want the numerator P(x) would be zero at x= -2 and x= 1, providing
assigned x-intersectios. So we take the numersator P(x) as a quadratic function
P(x) = a*(x-(-2))*(x-1) = a*(x+2)*(x-1).
Now the ratio 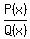 will have the assigned x-intersections and
assigned vertical asymptotes.
To have the given horizontal asymptote y= 2 at x -- +/- will have the assigned x-intersections and
assigned vertical asymptotes.
To have the given horizontal asymptote y= 2 at x -- +/-  , we take a = -2.
So, finally our rational function is R(x) = , we take a = -2.
So, finally our rational function is R(x) = 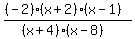 . ANSWER . ANSWER
Solved, answered and explained.
You can re-write the answer in any other equivalent form, if you want or if you need.
|
|
|