|
Question 1195991: Find the range of f(x) = (x-3)/(sqrt(3-sqrt(x+2))
Found 3 solutions by ikleyn, greenestamps, math_tutor2020:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the range of 
(1) The numerator is monotonically increasing;
(2) The denominator is monotonically decreasing
Therefore, the function is monotonically increasing.
Because of the 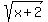 in the denominator, the minimum value for x is -2. Then, since the function is monotonically increasing, the minimum value of the function is in the denominator, the minimum value for x is -2. Then, since the function is monotonically increasing, the minimum value of the function is  = -2.88675 to 5 decimal places. = -2.88675 to 5 decimal places.
The denominator of the function is positive, because it is of the form sqrt(A). The value of x that makes the denominator 0 is x=7; so x must be less than 7.
But as x approaches 7 from the left, the denominator gets arbitrarily close to zero; and that means the value of the function gets arbitrarily large.
So there is no maximum value of the function.
ANSWER: The range of the function is from 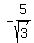 to infinity. to infinity.
Here is a graph of the function on the window [-3,8,-5,50], showing the minimum value of the function at (-2,-2.88675). Note that the graph is so steep close to x=7 that the graphing utility can't graph the function past a certain point, making it appear that the function has a maximum value.

But here is a graph of the function on the window [6.99,7,0,1000], showing that the function value is still increasing.

Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I want to expand on what the tutor @greenestamps wrote when he said the following
(1) The numerator is monotonically increasing;
(2) The denominator is monotonically decreasing
Therefore, the function is monotonically increasing.
The idea is this:
Consider a number C = A/B where B is nonzero.
If A goes up and B goes down, then C goes up
Example:
A = 12
B = 2
A/B = 12/2 = 6
A+1 = 12+1 = 13
B-1 = 2-1 = 1
We have C = A/B = 12/2 = 6 turn into C = (A+1)/(B-1) = 13/1 = 13
In short we have gone from 6 to 13 to show an overall increase.
This one example to show the claim above is correct. That claim being the overall function is monotonically increasing.
A more rigorous proof is required to fully verify the claim of course, but the example hopefully helps illustrate what is going on.
Monotonic means the function is always moving in one direction. Though the graph may have some sub-intervals as flat. This is where the graph is neither increasing nor decreasing.
In some math textbooks, the requirement is that there aren't any flat portions. However, the same idea applies in that the curve is either always going upward or always going downward.
A non-example of a monotonic function would be something like y = x^2. The left half decreases while the right side increases. The entire curve itself isn't doing the same thing over the domain.
|
|
|
| |