SOLUTION: Two billiard balls with similar mass have velocities of 3.0 m/s (ball 1) and -2.0 m/s (ball 2) when they meet in an elastic head‑on collision. What is the final velocity of the f

Since the collision is ELASTIC, you should apply two conservation laws.

First conservation law is the momentum conservation.
Second conservation law is the mechanical energy conservation.


So, let x be the final velocity of the 1-st ball after collision in m/s,
and let y the final velocity of the 2-nd ball after collision.

The masses of the balls are equal (as it is given). Let m be their mass (in kilograms).


The total momentum before collision was  3m - 2m = m (m*kg/s).
After collision, it remains the same, so we can write 
the momentum conservation equation in the form

    mx + my = m.

After reducing/canceling the common factor "m" in both sides, this equation takes the form

    x + y = 1   m/s    (1)


The total mechanical energy before collision was 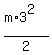  + 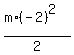 =  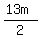 joules.
After collision, it remains the same, so we can write 
the mechanical energy conservation equation in the form

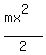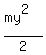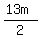     +  =   joules.

After reducing/canceling the common factor " 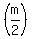 " in both sides, this equation takes the form

     +  = 13   (m/s)^2    (2)


Thus you have a system of two equations (1) and (2).


To solve it, express  y = 1-x  from equation (1) and substitute it into equation (2).
You will get then

    x^2 + (1-x)^2 = 13.


Simplify and find x

    x^2 + 1 - 2x + x^2 = 13

    2x^2 - 2x - 12 = 0

    x^2  -  x -  6 = 0

    (x-3)*(x+2) = 0.


It has two solution:  x = 3  and  x = -2.

We should carefully analyze these solutions.


(a)  If x= 3,  then  y= 1-x = -2.

     It means that velocities after collision are the same as before collision:
     it is as if the balls "penetrate" through each other without the collision,
     "not noticing each other".


     Notice that the equations formally ADMIT such a possibility --- but it is CLEARLY 
     not physical solution/situation.


(b)  If x= -2, then y= 1-x = 1 - (-2) = 3.


     Physically, it means that the balls EXCHANGE with their velocities,
     and it is exactly what an observer may expect at elastic collision 
     of two balls of equal masses. 


ANSWER.  After collision, 1st ball's velocity is -2 m/s; 2nd ball's velocity is 3 m/s.