Question 1195918: This is a calculus question. Can you explain each choice of #4 on https://www.math.purdue.edu/php-scripts/courses/oldexams/serve_file.php?file=16200E3-F2018.pdf ?
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(I) At small values of real positive quantity x, ln(1+x) is equivalent to x
as a small quantity in Calculus.
Even more precisely, 0 < 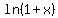 <= x
THEREFORE, 0 < <= x
THEREFORE, 0 <  <= <=  .
The series .
The series  is convergent, which is well known fact in Calculus after Euler.
So, the series is convergent, which is well known fact in Calculus after Euler.
So, the series  is convergent, too.
(II) When x is small, sin(x) is equivalent to x as a small quantity in Calculus.
Therefore, is convergent, too.
(II) When x is small, sin(x) is equivalent to x as a small quantity in Calculus.
Therefore,  is equivalent to is equivalent to  .
The series .
The series  is harmonic series, and it is divergent - which is
a well known fact in Calculus.
It implies that the series is harmonic series, and it is divergent - which is
a well known fact in Calculus.
It implies that the series  is divergent, too.
(III) Estimate is divergent, too.
(III) Estimate  = =  is equivalent to n^(3/2)*(1/(2n^3)) = (1/2)*(1/n^(3/2)).
Therefore, it is OBVIOUS that the series is equivalent to n^(3/2)*(1/(2n^3)) = (1/2)*(1/n^(3/2)).
Therefore, it is OBVIOUS that the series  is convergent.
Thus we have this conclusion: series (I) converges; series (II) diverges; series (III) converges.
ANSWER. Option (B). is convergent.
Thus we have this conclusion: series (I) converges; series (II) diverges; series (III) converges.
ANSWER. Option (B).
Solved.
/////////////////
Comment from student: Thank you. I am confused on the step that you explained (I took a screenshot of it):
https://drive.google.com/file/d/1SMF_1rbZAQCY0SzU_9WfjtzSff8WLDbC/view?usp=sharing
How did you manipulate algebraically?
My response: the question is to explain why
 is equivalent to is equivalent to 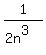 . (*) . (*)
Notice that in this problem n is a BIG value; so, 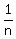 and and 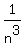 are small quantities. are small quantities.
In Calculus, if " a " is a small value, then
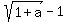 is equivalent, in order of smallness, to is equivalent, in order of smallness, to  . (**) . (**)
It is from the area of common knowledge in Calculus.
So, our estimate (*) is a direct consequense of (**).
\\\\\\\\\\\\\\
If you seriously want to understand the solutions of this problem and other similar problems
from your list, you should be FREE in manipulating basic knowledge of Calculus,
since they are PRE-REQUIZITES for solving such problems.
|
|
|