Question 1195897: How many different 11-letter arrangements can be made using the letters in the word FIRECRACKER?
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
The given word has 11 letters.
Of them, the letters "R", "E", and "C" are repeated and have multiplicity of 3, 2, and 2, respectively..
All other letters are unique.
To calculate the number of all distinguishable arrangements of the 11 letters, use the formula
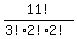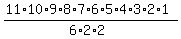 =  = 1663200. ANSWER
In this formula, 11! counts for all possible permutations, while the factor (3!)*(2!)*(2!) in the denominator
reduces undistinguishable permutations.
Solved.
--------------
To see many other similar (and different) solved problems, look into the lesson
- Arranging elements of sets containing indistinguishable elements
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|
