SOLUTION: About 20% of all professional foot ball players are injured during a given season a team has four star players a) what is the probability that at list two of the star players gets

This problem is a binomial distribution with the parameters

    n = 4    (the number of trials);

    k >= 2   (the number of success);

    p = 0.2  (the probability of individual success).


The probability is  

    P = P(2) + P(3) + P(4) = P(n=4, k>=2, p=0.2) =  = .


     To facilitate my calculations, I used online calculator at this site  https://stattrek.com/online-calculator/binomial.aspx

     It provides nice instructions  and  a convenient input and output for all relevant options/cases.


          The resulting number is P = 0.1808  (rounded).    ANSWER

The binomial distribution has the following properties:


    The mean of the distribution (μx) is equal to n * P  = 4*0.2 = 0.8.


    The variance (σ2x) is n * P * ( 1 - P ) = 4*0.2*0.8 = 0.64.


    The standard deviation (σx) is sqrt[ n * P * ( 1 - P ) ] = 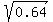 = 0.8.



For the reference,  see this web-site


https://stattrek.com/probability-distributions/binomial#:~:text=The%20binomial%20distribution%20has%20the,(%201%20%2D%20P%20)%20%5D.


or your textbook.