Question 1195834: How many ordered pairs of integers (a,b) satisfy all of the following inequalities?

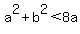
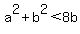
Found 3 solutions by greenestamps, ikleyn, math_tutor2020:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
*** Note that another tutor has pointed out that my solution below overlooks
*** two other solutions, (3,2) and (2,3) -- so there are 6 ordered pairs that
*** satisfy the given inequalities, not just 4.
First, notice that, by symmetry, if (m,n) satisfies all three conditions then (n,m) does also.
Next, since a^2 and b^2 are non-negative, conditions 2 and 3 mean a and b are positive; and condition 1 means a and b are both less than 4.
So we know a and b are both either 1, 2, or 3. There aren't a lot of ordered pairs to look at, so a "brute force" solution (by simply trying all the ordered pairs with both coordinates 1, 2, or 3) will be easier than a formal algebraic solution.
Trial and error show that (1,1) and (2,2) satisfy the conditions, but (3,3) violates condition 1.
Trial and error shows that (2,1) satisfies the conditions, so (1,2) does also. And similar trial and error shows that (3,1) and (1,3) do not satisfy all the conditions.
So we have found all the ordered pairs of integers that satisfy all three conditions: (1,1), (2,2), (1,2), and (2,1).
ANSWER: 4
You can easily verify this answer by using x and y instead of a and b and graphing all three equations (not the inequalities) on desmos.com. The ordered pairs that satisfy all three conditions are the lattice points that are inside all three circles.
Of course, you could also find the answer by doing the graphing first, without the logical analysis I showed in the first part of my response.
Answer by ikleyn(52818)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
@greenestamps has the right idea, but is missing (2,3) and (3,2) as solutions.
Verification using Desmos

Link to the interactive graph
https://www.desmos.com/calculator/jkunovtp9z
All of the points marked are inside all three circles simultaneously; hence they satisfy the three original inequalities.
Replace x with 'a', and replace y with 'b'.
Answer: 6 ordered pairs
|
|
|