Question 1195759: The radioactive element carbon-14 has a half-life of 5750 years. A scientist determined that the bones from a mastodon had lost 60.4% of their carbon-14. How old were the bones at the time they were discovered?
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52817)   (Show Source):
You can put this solution on YOUR website! .
The radioactive element carbon-14 has a half-life of 5750 years. A scientist determined that the bones
from a mastodon had lost 60.4% of their carbon-14. How old were the bones at the time they were discovered?
~~~~~~~~~~~~~~~~~~~
On solving similar problem, related to radioactive decay, see the lessons
- Radioactive decay problems
- Carbon dating problems
in this site.
Learn the subject from there.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
///////////////////////////////
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
The solution by @josgaithmetic in his post is INCORRECT from its first line
to the last line including the answer, which is WRONG, too.
In my post, I will bring a correct solution, and then at the end, will explain,
why everything in post by @josgarithmetic is wrong.
Since you are given half-life period, you do not need to write the exponential
decay function in the (ekt)-form and then to determine the parameter "k" of this form.
Write exponential decay function for the remaining mass using base 1/2 in the form
M(t) = 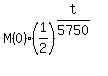 . (1)
It is the STANDARD exponential decay form function, when the half-life is given.
Next, in your problem, the lost mass of the carbon-14 is 60.4%.
It means that remaining mass of carbon-14 is 100%-60.4% = 39.6%.
THEREFORE, the equation (1) for the remaining mass takes the form
0.396 =  ,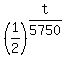
or, which is the same,
0.396 = 0.5^(t/5750). (2)
Take logarithm base 10 of both sides of (2). You will get
log(0.396) =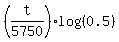 
which implies
t = 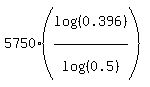 = 7684 years, or, rounding to closest one hundred years,
as usually people do in such calculations, we get the
ANSWER. The bones are 7700 years old.
Solved.
---------------------
The solution by @josgarithmetic has two errors.
First error is that he starts from (ekt)-form of the exponential decay function,
having given data about the half life period.
In such cases, the normal procedure is to use the base 1/2 exponential
function. Otherwise, you will make unnecessary calculations to find the coefficient "k"
of the exponential function, and, at the same time, you will demonstrate
that you are infamiliar with the regular procedure.
The second error in the solution by @josgarithmetic is that he uses given 60.4%
as the remaining mass, although the problem clearly states that it is the lost mass percentage.
*******************************************************************************
Everything related to the solution procedure for exponential equation,
when the half life is given, is described and clearly explained
in my lesson/lessons, to which I referred in my post above.
*******************************************************************************
After my post, @josgarithmetic changed/corrected his calculations, related to the remaining mass.
Answer by josgarithmetic(39621)  (Show Source):
|
|
|
