SOLUTION: A group of 15 individuals is used for a biological case study. The group contains 3 people with blood type O, 5 with blood type A, 4 with blood type B, and 3 with blood type AB. Wh

Algebra ->  Probability-and-statistics -> SOLUTION: A group of 15 individuals is used for a biological case study. The group contains 3 people with blood type O, 5 with blood type A, 4 with blood type B, and 3 with blood type AB. Wh      Log On


   

Question 1195514: A group of 15 individuals is used for a biological case study. The group contains 3 people with blood type O, 5 with blood type A, 4 with blood type B, and 3 with blood type AB. What is the probability that a random sample of 7 will contain 2 persons with blood type O, 2 persons with blood type A, 2 persons with blood type B, and 1 person with blood type AB?

Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!

        number of favorable outcomes
  P = ---------------------------------
      total number of possible outcomes

The favorable outcomes are choosing 2 of the 3 people with type O, AND 2 of the 5 with type A, AND 2 of the 4 with type B, AND 1 of the 3 with type AB:

C%283%2C2%29%2AC%285%2C2%29%2AC%284%2C2%29%2AC%283%2C1%29

The possible outcomes are choosing any 7 of the 15 people:

C%2815%2C7%29

ANSWER: %28C%283%2C2%29%2AC%285%2C2%29%2AC%284%2C2%29%2AC%283%2C1%29%29%2FC%2815%2C7%29

Use a calculator....

Answer by ikleyn(52786) About Me  (Show Source):
You can put this solution on YOUR website!
.
A group of 15 individuals is used for a biological case study.
The group contains 3 people with blood type O, 5 with blood type A,
4 with blood type B, and 3 with blood type AB.
What is the probability that a random sample of 7 will contain
2 persons with blood type O, 2 persons with blood type A,
2 persons with blood type B, and 1 person with blood type AB?
~~~~~~~~~~~~~~~ 

This problem is solved in two steps.


First step is to compute the number of all possible different groups of 7
individuals that can be formed/selected from 15 individuals.


This number is the number of combinations of 15 individuals taken 7 at a time

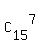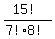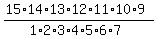    C%5B15%5D%5E7 = %2815%21%29%2F%287%21%2A8%21%29 = %2815%2A14%2A13%2A12%2A11%2A10%2A9%29%2F%281%2A2%2A3%2A4%2A5%2A6%2A7%29 = 6435.


Second step is to compute the number of favorable groups of 7 individuals with given compositions.


Two persons with blood type  O can be chosen from 3 people with blood type  O by C%5B3%5D%5E2 = 3 different ways.

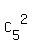Two persons with blood type  A can be chosen from 5 people with blood type  A by C%5B5%5D%5E2 = 10 different ways.

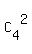Two persons with blood type  B can be chosen from 4 people with blood type  B by C%5B4%5D%5E2 = 6 different ways.

One person  with blood type AB can be chosen from 3 people with blood type AB by C%5B3%5D%5E1 = 3 different ways.


So,  3*10*6*3 = 540  different groups can be formed of the given composition.


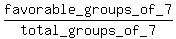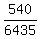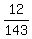Then the probability under the problem's question is  P = favorable_groups_of_7%2Ftotal_groups_of_7 = 540%2F6435 = 12%2F143.


ANSWER.  The probability that a random sample of 7 will contain 
         2 persons with blood type O, 2 persons with blood type A, 
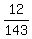         2 persons with blood type B, and 1 person with blood type AB is  12%2F143 = 0.0839 (rounded).

Solved.