SOLUTION: 4. A friend offers you the following game: You will roll two fair dice. If the sum of the two numbers obtained is 2, 3, 4, 9, 10, 11, or 12, your friend will pay you $20. However,

Algebra ->  Probability-and-statistics -> SOLUTION: 4. A friend offers you the following game: You will roll two fair dice. If the sum of the two numbers obtained is 2, 3, 4, 9, 10, 11, or 12, your friend will pay you $20. However,       Log On


   

Question 1195436: 4. A friend offers you the following game: You will roll two fair dice. If the sum of the two numbers obtained is 2, 3, 4, 9, 10, 11, or 12, your friend will pay you $20. However, if the sum of the two numbers is 5, 6, 7 or 8, you will pay your friend $20. Your friend points out that you have seven winning numbers and only four losing numbers. Is this game fair to you? Should you accept this
offer? Support your conclusion with the appropriate calculation.

Answer by ikleyn(52864) About Me  (Show Source):
You can put this solution on YOUR website!
.
4. A friend offers you the following game: You will roll two fair dice.
If the sum of the two numbers obtained is 2, 3, 4, 9, 10, 11, or 12, your friend will pay you $20.
However, if the sum of the two numbers is 5, 6, 7 or 8, you will pay your friend $20.
Your friend points out that you have seven winning numbers and only four losing numbers.
Is this game fair to you? Should you accept this
offer? Support your conclusion with the appropriate calculation.
~~~~~~~~~~~~~~~~~~ 

In each game, there are 6*6 = 36 possible outcomes. 
They are the pairs (a,b), where a and b are integer numbers from 1 to 6, inclusive,
Each possible pair goes with the probability of 1/36.


P(a+b = 2) = 1/36     ( the only winning pair (a,b) is (1,1) ).

P(a+b = 3) = 2/36     ( the winning pairs (a,b) are (1,2), (2,1) ).

P(a+b = 4) = 3/36     ( the winning pairs (a,b) are (1,3), (2,2), (3,1) ).

P(a+b = 9) = 4/36     ( the winning pairs (a,b) are (3,6), (4,5), (5,4), (6,3) ).    

P(a+b = 10) = 3/36    ( the winning pairs (a,b) are (4,6), (5,5), (6,4) ).    

P(a+b = 11) = 2/36    ( the winning pairs (a,b) are (5,6), (6,5) ).    

P(a+b = 12) = 1/36    ( the only winning pair (a,b) is (6,6) ).

---------------------------

So, P(the sum is 2,3,4,9,10,11 or 12) = 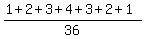%281%2B2%2B3%2B4%2B3%2B2%2B1%29%2F36 = 16/36 = 4/9.


From the other hand side, P(the sum is 5, 6, 7 or 8) is the complement to it, i.e. 1 - 4/9 = 5/9.


Thus the game is not fair: playing many time, you will lose %281%2F9%29%2A20 dollars each game, in average.

Solved.

---------------

On rolling dice problems see the lesson
    - Rolling a pair of fair dice
in this site.  You will find there many similar solved problems.


Read it and learn the subject from there.  After that,  you will be able easy solve such problems
ON  YOUR  OWN,  which is your  MAJOR  GOAL  visiting this forum  (I believe).


Also,  you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this online textbook under the topic  "Solved problems on Probability".


Save the link to this textbook together with its description

Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson

into your archive and use when it is needed.