

 let
let 

 let
let 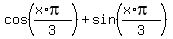

 Substituting:
Substituting:


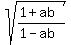 Under the radical multiply top and bottom by the conjugate
of the denominator, as if you were rationalizing the denominator:
Under the radical multiply top and bottom by the conjugate
of the denominator, as if you were rationalizing the denominator:





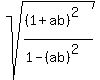 The numerator is a perfect square, so we take the square root of
the numerator and denominator:
The numerator is a perfect square, so we take the square root of
the numerator and denominator:


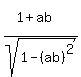 Write the right side as the sum of two fractions:
Write the right side as the sum of two fractions:


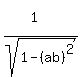

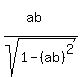 Next we draw a right triangle with an angle θ, 1 as the hypotenuse, ab
as the adjacent side and the radical as the opposite side:
Next we draw a right triangle with an angle θ, 1 as the hypotenuse, ab
as the adjacent side and the radical as the opposite side:
 So now the equation is
So now the equation is




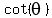 where
where 

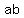 Since you want y as a function of cot(θ), we use an identity for csc(θ).
1 + cot2(θ) = csc2(θ), solve for csc(θ)
Since you want y as a function of cot(θ), we use an identity for csc(θ).
1 + cot2(θ) = csc2(θ), solve for csc(θ)


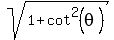 And we substitute back for ab:
The final equation is
And we substitute back for ab:
The final equation is


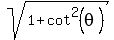

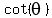 where
where 

 Edwin
Edwin