Question 1195353: A particle travelling in a straight line passes a fixed point O with a velocity of 16 m/s. Its
acceleration, a m/s^2, is given by a = 12- 6t, where t is the time in seconds after passing O. Calculate
a) the greatest speed attained by the particle in the original direction of the motion.
b) The distance from O when t = 2
Answer by Edwin McCravy(20060)   (Show Source):
You can put this solution on YOUR website! A particle travelling in a straight line passes a fixed point O with a velocity of 16 m/s. Its
acceleration, a m/s^2, is given by a = 12- 6t, where t is the time in seconds after passing O. Calculate
a) the greatest speed attained by the particle in the original direction of the motion.
b) The distance from O when t = 2
  
   
  
    
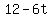
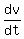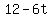
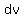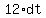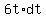
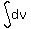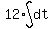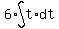
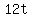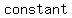When t=0, the particle is at O, with velocity 16. So we substitute
t=0 and v=16
  
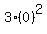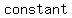So the constant is 16, and
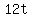Use the vertex formula or differentiating and setting the derivative = 0
to find that the maximum velocity is
v=28 m/s when t=2 seconds. <--answer to (a)
To find the distance when t=2,
   
   
    
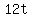
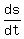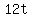
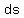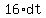
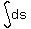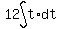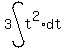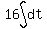
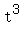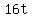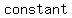When t=0, the particle is at O, so at that instant the distance s=0, So
we substitute t=0 and s=0
   
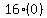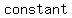So the constant is 0
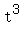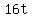We substitute t=2
  
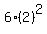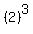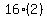s = 48 meters. <--answer to (b)
Edwin
|
|
|
