Question 1195309: A sphere and a right circular cylinder have equal volumes. The radius of the sphere equals the radius of the base of the cylinder. Compare the surface area of the sphere with the area of the total surface of the cylinder.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
The volume of a sphere is  with r being the radius.
The volume of a cylinder is 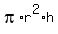 where h is the height.
For each 3D object, the r value is the same number.
We're told those two 3D objects have the same volume.
Equate those two expressions and let's solve for h.
 The pi terms cancel when we divide both sides by pi
 Divide both sides by r^2
Now plug this into the expression for the volume of the cylinder.
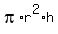
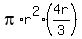
We end up with the volume of a sphere, which helps confirm we have the correct h value.
----------------------------------------------------------
The surface area of a sphere with radius r is 
The surface area of a cylinder is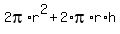 
Plug in and simplify
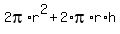
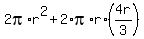
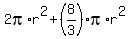
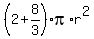
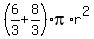
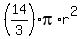
This represents the surface area of a cylinder such that h = 4r/3, which was derived from the fact the cylinder and sphere have the same volume.
----------------------------------------------------------
We found that...- surface area of a sphere is
- surface area of a cylinder is
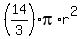
with both having the same volume.
If you were to divide the two expressions, then the pi and r^2 terms cancel out. It doesn't matter if the order is sphere/cylinder or if you did cylinder/sphere.
If you did sphere/cylinder, then 4 divided by (14/3) becomes 12/14 which reduces to 6/7
It tells us the ratio of the sphere's area to the cylinder's area is 6:7
For instance, if we knew the sphere had a surface area of 60 square cm, then the cylinder must have a surface area of 70 square cm. The values form the ratio 60:70 and it simplifies to 6:7.
If you did cylinder/sphere instead, then you'd arrive at 7:6 as the ratio of the cylinder area to the sphere area.
Once again, this only works when the two volumes are the same. And also they must have the same radius.
----------------------------------------------------------
Another perspective:
Start with the expression 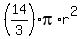which was the surface area of the cylinder, that has equal volume to the sphere.
It looks very similar to (surface area of a sphere), but we have the 14/3 out front rather than just 4.
The motivation is that we want to multiply the 4 by some multiplier x, to arrive at 14/3
4x = 14/3
x = (14/3)*(1/4)
x = 14/12
x = 7/6
Telling us that 4 times 7/6 will get us to 14/3
So,
cylinder area = (7/6)*(sphere area)
which can be rephrased as
sphere area = (6/7)*(cylinder area)
Answer by ikleyn(52903)  (Show Source):
You can put this solution on YOUR website! .
I don't know what the word " compare " means in this problem.
It is very possible that it simply asks what area is greater/smaller without making any calculations.
If so, then it is useful to know that
of all solids with the given volume, a sphere has minimal surface area.
It is similar to that as for all plane shapes with the given area a circle has minimal perimeter.
It is also similar to that as for all rectangles with the given area a square has minimal perimeter.
|
|
|
