Question 1195271: Let P(x)=2009x^9+a₁x^8+...+a₉ such that
 , n = 1,2,...,9. , n = 1,2,...,9.
Find 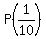 . .
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52792)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let P(x) = 2009x^9 + a₁x^8 + . . . + a₉ such that
 , n = 1,2,...,9. , n = 1,2,...,9.
Find 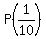 . .
~~~~~~~~~~~~~~~~~
The solution by @MathLover1 is INCORRECT and IRRELEVANT.
Do not spend your time looking in it; I also will not spend my and your time,
explaining why it is wrong and irrelevant.
Simply madam does not understand the problem, does not know the subject
and is not in the theme.
Read my solution below.
You are given a polynomial P(x) of degree 9 with the leading coefficient 2009;
all 9 coefficients of lower degrees are unknown.
You also are given the values of the polynomial in 9 points
P(1) = 1, 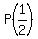 = = 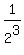 , , 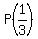 = = 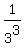 , . . . , , . . . , 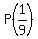 = = 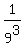 .
Consider another polynomial
Q(x) = .
Consider another polynomial
Q(x) = 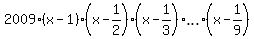 + +  .
This polynomial has the degree of 9 and has the same values 1, .
This polynomial has the degree of 9 and has the same values 1, 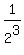 , , 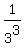 , . . . , , . . . , 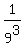 in all 9 given points 1,
in all 9 given points 1,  , ,  , . . . , , . . . , 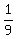 , as polynomial P(x) has.
You can easily see it from the formula.
In addition, polynomial Q(X) has the same value
of the leading coefficient 2009 as polynomial P(X) has.
It , as polynomial P(x) has.
You can easily see it from the formula.
In addition, polynomial Q(X) has the same value
of the leading coefficient 2009 as polynomial P(X) has.
It  that polynomials P(x) and Q(X) are identical as polynomials of x.
THEREFORE, that polynomials P(x) and Q(X) are identical as polynomials of x.
THEREFORE, 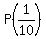 = = 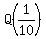 = = 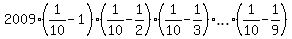 + +  .
This expression is the .
This expression is the   to the problem. to the problem.
Solved, answered, explained and completed.
///////////////
This problem is of a Math Olympiad level or an advanced Math Circle level,
and my solution is written adequately to this level.
|
|
|