Question 1195240: The table below shows the scores of a group of students on a 10-point quiz.
Test Score-3,4,5,6,7,8,9,10
Frequency-0,5,2,1,1,2,4,0
The mean score on this test is:
The median score on this test is:
Found 2 solutions by MathLover1, math_tutor2020:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Test Score:  , , , , , , , , , , , , , ,
Frequency: , , , , , , , , , , , , , ,
as you an see there is  scores of scores of  and and 
Scores are:
 , , , , , , , , , , , , , , , , , , , , , ,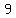 , , , ,
The mean score on this test is: 
The median score is the score in the middle: 
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answers:
Mean = 6.333 (approximate)
Median = 6
====================================================
Explanation:
We'll start off finding the mean.
Here's the original data table
| Score | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | Frequency | 0 | 5 | 2 | 1 | 1 | 2 | 4 | 0 |
Let's introduce a third row where we multiply the items in each separate column.
Example: 4*5 = 20 in the second column
| Score | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | Frequency | 0 | 5 | 2 | 1 | 1 | 2 | 4 | 0 | | Score*Frequency | 0 | 20 | 10 | 6 | 7 | 16 | 36 | 0 |
Add up those results from the third row:
0+20+10+6+7+16+36+0 = 95
Divide this over the total frequency (n = 0+5+2+1+1+2+4+0 = 15)
So we get 95/15 = 6.333 as the approximate mean
The slightly longer method is to have five copies of "4", two copies of "5", etc etc as the tutor @MathLover1 points out. While this longer method is fine, it gets a bit tedious if you had a larger table and/or higher frequencies. Imagine if one frequency was something like 50, which indicates you'd have to add 50 copies of the same number. It's more efficient to use multiplication.
-------------
Now to find the median.
As mentioned earlier, we have n = 15 as the total frequency
Half of which is n/2 = 15/2 = 7.5 which rounds to 8
The median is in slot 8
7 items are below the median, and 7 are above it
7+1+7 = 15 items total
Side note: This trick only works if n is odd.
Add the first two frequencies to get: 0+5 = 5
This partial sum is not 8 or larger
Add the first three frequencies: 0+5+2 = 7
This is not 8 or larger
Add the first four frequencies: 0+5+2+1 = 8
We arrive at 8 finally
Therefore, the score of 6 must be the median since that last frequency corresponds to the score of 6.
If you are following @MathLover1's method, then the data set {4, 4, 4, 4, 4, 5, 5, 6, 7, 8, 8, 9, 9, 9, 9} has the median of 6.
It's probably helpful to write on a scratch piece of paper that large set. Then repeatedly cross off the outer pair of items until things narrow down to the center-most number.
This is what the steps could look like. Take note of the color coding to see how the terms pair up and cancel.

Or you could have it written out like this
{4, 4, 4, 4, 4, 5, 5, 6, 7, 8, 8, 9, 9, 9, 9}
{4, 4, 4, 4, 5, 5, 6, 7, 8, 8, 9, 9, 9}
{4, 4, 4, 5, 5, 6, 7, 8, 8, 9, 9}
{4, 4, 5, 5, 6, 7, 8, 8, 9}
{4, 5, 5, 6, 7, 8, 8}
{5, 5, 6, 7, 8}
{5, 6, 7}
{6}
At some point, say possibly the second to last or third to last step, the median is probably easy to spot and there's no need to get to the final step shown above.
Or perhaps it's much easier to cancel in batches, like say cross off 2 at a time (at least until it's not possible to cancel in groups of 2 each)

It's up to you decide which method you prefer best.
Like with finding the mean, the long method of finding the median like this isn't too bad as long as the frequencies aren't too large. Luckily having 15 items isn't too bad. If n was larger, then I recommend using the trick involving partial sums to locate the median.
|
|
|